Table des matières of 11.2 Mesures

Comme nous venons de le voir, le but de la tomographie par rayons X est de trouver la fonction d'atténuation f $\left(\vphantom{x,y}\right.$ x, y $\left.\vphantom{x,y}\right)$ . Pour atteindre cet objectif, on effectue tout d'abord des mesures qui fournissent des équations mathématiques faisant intervenir f $\left(\vphantom{x,y}\right.$ x, y $\left.\vphantom{x,y}\right)$ . Ensuite, on résout ces équations pour obtenir f $\left(\vphantom{x,y}\right.$ x, y $\left.\vphantom{x,y}\right)$ .

Dans les scanners à rayons X, l'information accessible sur f $\left(\vphantom{x,y}\right.$ x, y $\left.\vphantom{x,y}\right)$ se présente sous la forme d'intégrales de f $\left(\vphantom{x,y}\right.$ x, y $\left.\vphantom{x,y}\right)$ sur différentes droites du plan $\left(\vphantom{x,y}\right.$ x, y $\left.\vphantom{x,y}\right)$ . On parle d'intégrales de lignes. La figure 11.3 illustre la situation. Conceptuellement, on utilise une source de rayons X et un détecteur (compteur) de photons. La source envoie un faisceau de N_i photons dans la direction du détecteur au travers de la coupe, on détermine le nombre N_o de photons qui passent, puis, par le biais de la relation $\Delta$ N = - f N $\Delta$ l, on trouve

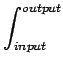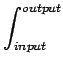$\displaystyle \int_{{input}}^{{output}}$ $\displaystyle {\frac{{dN}}{{N}}}$ = - $\displaystyle \int_{{input}}^{{output}}$ f $\displaystyle \left(\vphantom{x,y}\right.$ x, y $\displaystyle \left.\vphantom{x,y}\right)$ dl $\displaystyle \rightarrow$ log $\displaystyle \left(\vphantom{\frac{N_{i}}{N_{o}}}\right.$ $\displaystyle {\frac{{N_{i}}}{{N_{o}}}}$ $\displaystyle \left.\vphantom{\frac{N_{i}}{N_{o}}}\right)$ = $\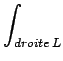displaystyle \int_{{droite\, L}}^{}$ f $\displaystyle \left(\vphantom{x,y}\right.$ x, y $\displaystyle \left.\vphantom{x,y}\right)$ dl

(11.1)

Pour calculer (reconstruire) f $\left(\vphantom{x,y}\right.$ x, y $\left.\vphantom{x,y}\right)$ de façon exacte, nous verrons que les intégrales de lignes de f $\left(\vphantom{x,y}\right.$ x, y $\left.\vphantom{x,y}\right)$ doivent être connues pour toutes les droites qui passent au travers de la coupe étudiée.

Il y a deux façons différentes de collecter les mesures sur l'ensemble des droites passant au travers de la coupe: en géométrie parallèle (voir la figure 11.4) et en géométrie en éventail (voir la figure 11.5).

**Figure 11.4:** Acquisition des mesures en géométrie parallèle.

**Figure 11.5:** Acquisition des mesures en géométrie en éventail.

En géométrie parallèle, les mesures log $\left(\vphantom{N_{i}/N_{o}}\right.$ N_i/N_o $\left.\vphantom{N_{i}/N_{o}}\right)$ sont réalisées sur des ensembles de droites parallèles. On déplace la source et le détecteur dans une direction donnée $\vec{{\theta}}\,$ pour obtenir les mesures sur toutes les droites perpendiculaires au vecteur $\vec{{\theta}}\,$ . Ensuite, on applique une rotation à l'ensemble source-détecteur afin d'obtenir des nouvelles mesures en répétant le mouvement de translation. Le mouvement de rotation s'effectue sur un intervalle angulaire de longueur $\pi$ .

En géométrie en éventail, on utilise tout un banc de détecteurs. La source envoie simultanément ses rayons en direction de tous les détecteurs de ce banc de telle sorte que l'on obtient pour une position angulaire donnée tout un jeu de mesures correspondant à des droites formant un éventail. Pour couvrir toutes les droites du plan, on considère généralement un mouvement de rotation de l'ensemble source-banc sur un intervalle de longueur 2 $\pi$ , ce qui, notons-le, conduit à une redondance d'ordre 2 dans les mesures. Par rapport à la géométrie parallèle, on observe que la géométrie en éventail permet une acquisition plus rapide des données, grâce à la suppression du mouvement de translation.

Conceptuellement, l'appareillage requis pour la géométrie en éventail est plus coûteux que celui requis pour la géométrie parallèle. Toutefois, la géométrie en éventail est préférée à la géométrie parallèle car elle permet d'acquérir les mesures plus rapidement. La vitesse d'acquisition des mesures est de fait un facteur très important en tomographie. Dans la discussion ci-dessus, nous avons fait l'hypothèse implicite que la fonction f $\left(\vphantom{x,y}\right.$ x, y $\left.\vphantom{x,y}\right)$ ne varie pas au cours du temps. Lorsque le patient bouge durant l'acquisition des mesures (ne serait-ce qu'en respirant), l'expression de f $\left(\vphantom{x,y}\right.$ x, y $\left.\vphantom{x,y}\right)$ peut changer d'une intégrale de ligne à une autre et la qualité des images obtenues est alors médiocre. Les scanners actuels utilisent la géométrie en éventail et peuvent collecter les mesures pour une coupe donnée en moins de 750 $\left[\vphantom{ms}\right.$ ms $\left.\vphantom{ms}\right]$ , de telle sorte que le patient ne bouge pratiquement pas.

Pour la formulation mathématique du problème de reconstruction de f $\left(\vphantom{x,y}\right.$ x, y $\left.\vphantom{x,y}\right)$ à partir de ses intégrales de lignes, notons qu'il est plus facile de travailler en géométrie parallèle, comme effectué ci-après.