La méthode de rétroprojection des projections filtrées se déduit de
l'observation suivante: l'image
fB(![]() ) dans la méthode
du filtrage de la rétroprojection est non-nulle en-dehors du support
de
f (
) dans la méthode
du filtrage de la rétroprojection est non-nulle en-dehors du support
de
f (![]() ), et donc diffère de
f (
), et donc diffère de
f (![]() ), uniquement parce
que les mesures
g(
), uniquement parce
que les mesures
g(![]() , s) sont strictement positives. Avant d'effectuer
l'opération de rétroprojection, il faut effectuer un rehaussement
des hautes fréquences dans les projections afin d'y introduire des
composantes négatives. De cette façon, on peut espérer une certaine
compensation de valeurs lors de l'étape de rétroprojection, pour obtenir
une image qui est plus proche de
f (
, s) sont strictement positives. Avant d'effectuer
l'opération de rétroprojection, il faut effectuer un rehaussement
des hautes fréquences dans les projections afin d'y introduire des
composantes négatives. De cette façon, on peut espérer une certaine
compensation de valeurs lors de l'étape de rétroprojection, pour obtenir
une image qui est plus proche de
f (![]() ), avec des valeurs nulles
en-dehors du support de
f (
), avec des valeurs nulles
en-dehors du support de
f (![]() ). La figure 11.14 illustre
la situation.
). La figure 11.14 illustre
la situation.
On utilise l'expression mathématique
| fh( |
(11.13) |
Le filtre h(s) s'obtient à partir de la relation entre
fh(![]() )
et
f (
)
et
f (![]() ). Suivant les mêmes étapes de calcul qu'à la section
précédente, on trouve en effet que
). Suivant les mêmes étapes de calcul qu'à la section
précédente, on trouve en effet que
fh(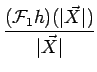 |
(11.14) |
À partir de cette relation, on voit qu'il suffit de choisir h(s)
tel que
(![]() 1h)(
1h)(![]() ) = |
) = |![]() | pour obtenir une reconstruction
exacte. Notons que ce filtre de convolution est uniquement défini
au sens des distributions.
| pour obtenir une reconstruction
exacte. Notons que ce filtre de convolution est uniquement défini
au sens des distributions.
En pratique, la reconstruction exacte de
f (![]() ) n'est jamais
possible parce que les projections ne sont connues qu'avec un certain
pas d'échantillonnage
) n'est jamais
possible parce que les projections ne sont connues qu'avec un certain
pas d'échantillonnage ![]() s. Le mieux que l'on puisse obtenir
est une reconstruction avec résolution
s. Le mieux que l'on puisse obtenir
est une reconstruction avec résolution
![]() x =
x = ![]() y =
y = ![]() s
et le filtre h(s) doit être adapté pour prendre cet aspect en compte.
Cela conduit au choix suivant pour h(s):
s
et le filtre h(s) doit être adapté pour prendre cet aspect en compte.
Cela conduit au choix suivant pour h(s):
| ( |
(11.15) |
W(t) = 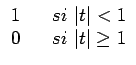 |
(11.16) |
| fh( |
(11.17) |
Finalement, notons que l'on peut choisir différentes expressions pour la fonction W(t), suivant le niveau de bruit dans les mesures. Lorsque les données sont bruitées, on modifie généralement l'expression de W(t) de façon à réduire la contribution des hautes fréquences et donc la propagation du bruit au sein de l'image. Les expressions typiquement choisies sont la fenêtre sinus cardinal (sinc),
W(t) = 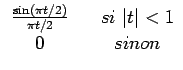 |
(11.18) |
W(t) =  |
(11.19) |
La figure 11.15 montre l'allure de
(![]() 1h)(
1h)(![]() )/
)/![]() pour les différents choix de W(t). La figure 11.16 montre
des résultats de reconstruction obtenus pour le fantôme de SHEPP-LOGAN
sur une grille de
256×256 pixels avec un sinogramme de taille
400×256, en utilisant successivement la fenêtre rectangulaire,
la fenêtre sinc, puis la fenêtre de HANNING.
pour les différents choix de W(t). La figure 11.16 montre
des résultats de reconstruction obtenus pour le fantôme de SHEPP-LOGAN
sur une grille de
256×256 pixels avec un sinogramme de taille
400×256, en utilisant successivement la fenêtre rectangulaire,
la fenêtre sinc, puis la fenêtre de HANNING.