-
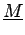 est symétrique si
est symétrique si
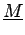 =
= 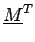
-
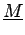 est orthogonale si
est orthogonale si
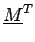
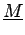 =
= 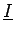 où
où
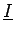 est la matrice identité.
est la matrice identité.
- Si
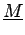 est symétrique, réelle
et orthogonale, alors
est symétrique, réelle
et orthogonale, alors
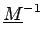 =
= 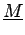
- Une matrice complexe
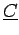 est hermitienne si
est hermitienne si
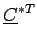 =
= 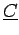 ,
où
,
où
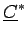 est la matrice complexe conjuguée de
est la matrice complexe conjuguée de
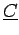 .
.
- Une matrice complexe
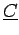 est unitaire
si
est unitaire
si
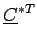
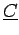 =
= 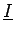
- Si
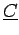 est une matrice complexe, carrée, hermitienne et
unitaire, alors
est une matrice complexe, carrée, hermitienne et
unitaire, alors
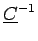 =
= 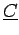
Revenons à présent aux matrices de transformation
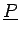 et
et
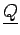 . Si
. Si
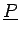 et
et
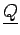 sont symétriques,
réelles et orthogonales, alors
sont symétriques,
réelles et orthogonales, alors
On parle alors de transformations orthogonales
ou unitaires. Les transformations
unitaires ont la propriété intéressante d'utiliser le même algorithme
pour la transformation inverse que pour la transformation directe.
Si les matrices
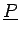 et
et
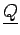 sont complexes, la
relation 2.6 tient toujours à condition que
sont complexes, la
relation 2.6 tient toujours à condition que
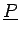 et
et
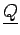 soient hermitiennes et unitaires.
soient hermitiennes et unitaires.
Marc Van Droogenbroeck. Tous droits réservés.
2003-09-30