2.8.1 Filtre passe-bas à fenêtre rectangulaire

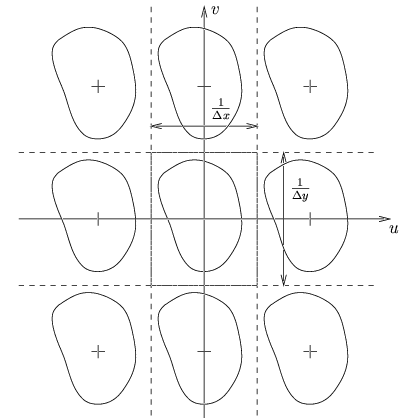
La fenêtre de filtrage a ici une forme rectangulaire. À la figure 2.10, on peut voir le spectre d'une fonction échantillonnée ainsi que la fenêtre rectangulaire de filtrage.

Figure 2.10: Filtre passe-bas à fenêtre rectangulaire
3525  

Le filtre est défini dans le domaine fréquentiel par la fonction de transfert suivante

$\displaystyle \mathcal {R}$$\displaystyle \left(\vphantom{u,v}\right.$u, v$\displaystyle \left.\vphantom{u,v}\right)$ = $\displaystyle \Delta$x$\displaystyle \Delta$yRect$\scriptstyle {\frac{{1}}{{\Delta x}}}$,$\scriptstyle {\frac{{1}}{{\Delta y}}}$$\displaystyle \left(\vphantom{u,v}\right.$u, v$\displaystyle \left.\vphantom{u,v}\right)$ (2.96)

On voit aisément que l'application de cette fenêtre fréquentielle à la fonction échantillonnée permet de reconstruire exactement f$ \left(\vphantom{x,y}\right.$x, y$ \left.\vphantom{x,y}\right)$. La réponse impulsionnelle du filtre s'obtient par transformée de FOURIER inverse de 2.96. Il vient

r$\displaystyle \left(\vphantom{x,y}\right.$x, y$\displaystyle \left.\vphantom{x,y}\right)$ = $\displaystyle {\frac{{\sin\left(\frac{\pi x}{\Delta x}\right)}}{{\frac{\pi x}{\Delta x}}}}$$\displaystyle {\frac{{\sin\left(\frac{\pi y}{\Delta y}\right)}}{{\frac{\pi y}{\Delta y}}}}$ (2.97)

En introduisant la notation de la fonction sinus cardinal, sinc$ \left(\vphantom{x}\right.$x$ \left.\vphantom{x}\right)$ = $ {\frac{{\sin\left(\pi x\right)}}{{\pi x}}}$, on peut encore écrire

r$\displaystyle \left(\vphantom{x,y}\right.$x, y$\displaystyle \left.\vphantom{x,y}\right)$ = sinc$\displaystyle \left(\vphantom{\frac{x}{\Delta x}}\right.$$\displaystyle {\frac{{x}}{{\Delta x}}}$$\displaystyle \left.\vphantom{\frac{x}{\Delta x}}\right)$sinc$\displaystyle \left(\vphantom{\frac{y}{\Delta y}}\right.$$\displaystyle {\frac{{y}}{{\Delta y}}}$$\displaystyle \left.\vphantom{\frac{y}{\Delta y}}\right)$ (2.98)

Ce filtre conduit a la formule de reconstruction suivante

fr$\displaystyle \left(\vphantom{x,y}\right.$x, y$\displaystyle \left.\vphantom{x,y}\right)$ = f$\displaystyle \left(\vphantom{x,y}\right.$x, y$\displaystyle \left.\vphantom{x,y}\right)$ = $\displaystyle \sum_{{i=-\infty}}^{{+\infty}}$$\displaystyle \sum_{{j=-\infty}}^{{+\infty}}$f$\displaystyle \left(\vphantom{i\Delta x,j\Delta y}\right.$i$\displaystyle \Delta$x, j$\displaystyle \Delta$y$\displaystyle \left.\vphantom{i\Delta x,j\Delta y}\right)$sinc$\displaystyle \left(\vphantom{\frac{x-i\Delta x}{\Delta x}}\right.$$\displaystyle {\frac{{x-i\Delta x}}{{\Delta x}}}$$\displaystyle \left.\vphantom{\frac{x-i\Delta x}{\Delta x}}\right)$sinc$\displaystyle \left(\vphantom{\frac{y-j\Delta y}{\Delta y}}\right.$$\displaystyle {\frac{{y-j\Delta y}}{{\Delta y}}}$$\displaystyle \left.\vphantom{\frac{y-j\Delta y}{\Delta y}}\right)$ (2.99)

Cette dernière formule constitue une formule d'interpolation qui permet de reconstruire exactement f$ \left(\vphantom{x,y}\right.$x, y$ \left.\vphantom{x,y}\right)$ à partir de ses échantillons f$ \left(\vphantom{i\Delta x,j\Delta y}\right.$i$ \Delta$x, j$ \Delta$y$ \left.\vphantom{i\Delta x,j\Delta y}\right)$. Cependant, il faut bien garder à l'esprit que cela n'est valable que si les conditions d'échantillonnage de SHANNON sont vérifiées. L'expression 2.99 est l'expression de la formule d'interpolation de WHITTAKER pour le cas des signaux à une dimension.

Marc Van Droogenbroeck. Tous droits réservés.
2003-09-30