Sous-sections
Contrairement au cas unidimensionnel, le traitement d'image offre
plus de liberté quant au choix du filtre passe-bas idéal. Il est ainsi
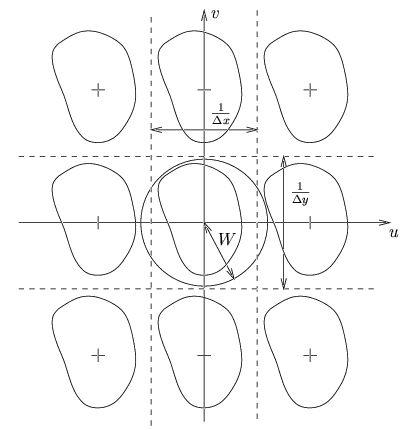
possible de choisir une fenêtre circulaire comme le montre la figure 2.11.
Figure 2.11:
Filtre passe-bas à fenêtre circulaire.
|
|
Il est clair que, pour que la reconstruction soit exacte, la fenêtre
circulaire doit contenir entièrement la réplique du spectre de
f x, y
x, y située à l'origine et elle ne peut intersecter les autres répliques
du spectre. Ce filtre est alors défini par la fonction de transfert
suivante
située à l'origine et elle ne peut intersecter les autres répliques
du spectre. Ce filtre est alors défini par la fonction de transfert
suivante
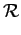 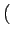 u, v u, v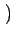 = = 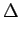 x x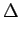 yDisqueW yDisqueW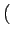 u, v u, v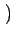 |
(2.100) |
La réponse impulsionnelle correspondante est donnée par
La formule de reconstruction ou d'interpolation est finalement
fr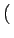 x, y x, y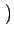 |
= |
f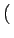 x, y x, y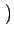 |
(2.102) |
| |
= |
W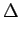 x x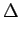 y y 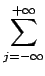 f f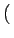 i i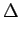 x, j x, j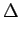 y y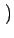 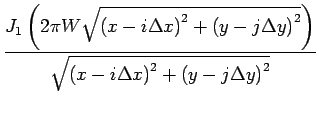 |
|
Cette dernière formule constitue une formule d'interpolation
faisant intervenir des fonctions de BESSEL du premier ordre.
Les fenêtres rectangulaire et circulaire ne sont pas les seules à
pouvoir être utilisées. Pour obtenir une reconstruction exacte de
f x, y
x, y , la fenêtre fréquentielle de filtrage doit vérifier
les conditions suivantes:
, la fenêtre fréquentielle de filtrage doit vérifier
les conditions suivantes:
- elle doit être symétrique par rapport à l'origine afin d'assurer que
l'image reconstruite soit réelle;
- elle doit contenir entièrement la réplique du spectre de
f
 x, y
x, y située à l'origine; et
située à l'origine; et
- elle ne peut intersecter les autres répliques du spectre de
f
 x, y
x, y .
.
À nouveau, il est bon de rappeler que tout ceci n'est valable que
si la fonction
f x, y
x, y est à bande limitée et que les
conditions d'échantillonnage sont vérifiées. Dans le cas contraire,
l'image reconstruite présentera ce qu'on appelle du repli de
spectre ou aliasing.
est à bande limitée et que les
conditions d'échantillonnage sont vérifiées. Dans le cas contraire,
l'image reconstruite présentera ce qu'on appelle du repli de
spectre ou aliasing.
Marc Van Droogenbroeck. Tous droits réservés.
2003-09-30
![]() x, y
x, y![]() située à l'origine et elle ne peut intersecter les autres répliques
du spectre. Ce filtre est alors défini par la fonction de transfert
suivante
située à l'origine et elle ne peut intersecter les autres répliques
du spectre. Ce filtre est alors défini par la fonction de transfert
suivante 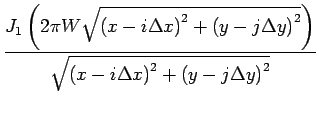
![]() x, y
x, y![]() , la fenêtre fréquentielle de filtrage doit vérifier
les conditions suivantes:
, la fenêtre fréquentielle de filtrage doit vérifier
les conditions suivantes: