Dans les deux sections précédentes, les filtres ont été définis dans
le domaine fréquentiel de l'image. Il est également possible de travailler
directement dans le domaine spatial, c'est-à-dire d'établir le filtre
de reconstruction
r x, y
x, y et de voir son effet dans le
domaine fréquentiel grâce à sa transformée de FOURIER
et de voir son effet dans le
domaine fréquentiel grâce à sa transformée de FOURIER

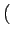 u, v
u, v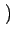 .
.
Considérons l'exemple suivant. Supposons que la fonction
f x, y
x, y ait été échantillonnée avec des pas
ait été échantillonnée avec des pas 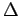 x et
x et 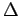 y constants.
Soit
fr
y constants.
Soit
fr x, y
x, y l'image reconstruite définie par
l'image reconstruite définie par
où i et j sont tels que
 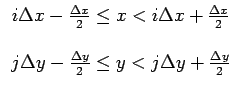 |
(2.104) |
Cette reconstruction correspond à l'interpolation du plus proche
voisin car la valeur de
fr en
 x, y
x, y correspond au plus proche échantillon
connu. L'image reconstruite peut donc être vue comme une image en
escaliers. Elle peut également s'écrire
correspond au plus proche échantillon
connu. L'image reconstruite peut donc être vue comme une image en
escaliers. Elle peut également s'écrire
fr x, y x, y = =  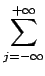 f f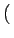 i i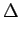 x, j x, j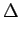 y y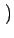 Rect Rect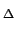 x, x,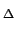 y y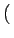 x - i x - i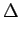 x, y - j x, y - j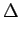 y y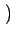 |
(2.105) |
De cette expression, nous pouvons extraire la fonction d'interpolation
(ou filtre de reconstruction) utilisée
r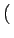 x, y x, y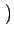 = Rect = Rect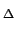 x, x,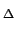 y y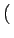 x, y x, y |
(2.106) |
Il est alors intéressant de regarder l'effet du filtre de reconstruction
sur l'image échantillonnée. Pour cela, observons la fonction de transfert
du filtre
Deux remarques importantes peuvent être faites à propos de ce filtre
de reconstruction:
- dans le plan fréquentiel
 u, v
u, v , la fenêtre de filtrage
, la fenêtre de filtrage

 u, v
u, v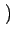 n'est pas constante sur tout le rectangle
de dimension
n'est pas constante sur tout le rectangle
de dimension
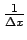 ×
×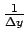 centré
à l'origine, c'est-à-dire la région contenant la réplique du spectre
de
f
centré
à l'origine, c'est-à-dire la région contenant la réplique du spectre
de
f x, y
x, y centrée à l'origine. Dans ce rectangle, les
composantes fréquentielles
centrée à l'origine. Dans ce rectangle, les
composantes fréquentielles
 u, v
u, v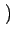 de l'image sont d'autant
plus atténuées que le couple
de l'image sont d'autant
plus atténuées que le couple
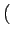 u, v
u, v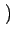 est éloigné de l'origine.
est éloigné de l'origine.
- la fenêtre fréquentielle n'est pas nulle en dehors de la région d'intérêt
rectangulaire de dimension
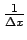 ×
×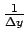 centrée à l'origine. L'image reconstruite tient non seulement compte
de la réplique du spectre de
f
centrée à l'origine. L'image reconstruite tient non seulement compte
de la réplique du spectre de
f x, y
x, y située à l'origine
mais en plus d'autres répliques qui vont introduire du repli de spectre
dans l'image reconstruite.
située à l'origine
mais en plus d'autres répliques qui vont introduire du repli de spectre
dans l'image reconstruite.
En toute généralité, l'utilisation de filtres de reconstruction non
idéaux (comme par exemple l'interpolation du plus proche voisin)
introduit les problèmes suivants:
- modification du contenu fréquentiel intrinsèque de l'image,
- introduction de hautes fréquences parasites dans l'image reconstruite.
Il existe évidemment d'autres filtres de reconstruction comme par
exemple l'interpolation linéaire par
morceaux (figure 2.12.a) ou l'interpolation
bilinéaire (figure 2.12.b).
Figure 2.12:
Exemples d'interpolateurs: (a) interpolation linéaire par morceaux,
(b) interpolation bilinéaire.
|
|
Insistons une fois encore sur la fait que l'utilisation d'un filtre
de reconstruction idéal ne fournira pas nécessairement une reconstruction
parfaite. Il faut pour cela que l'image
f x, y
x, y soit
à bande limitée (ce qui extrêmement rare en pratique) et échantillonnée
correctement (en concordance avec le théorème de SHANNON).
soit
à bande limitée (ce qui extrêmement rare en pratique) et échantillonnée
correctement (en concordance avec le théorème de SHANNON).
Marc Van Droogenbroeck. Tous droits réservés.
2003-09-30
![]() x, y
x, y![]() et de voir son effet dans le
domaine fréquentiel grâce à sa transformée de FOURIER
et de voir son effet dans le
domaine fréquentiel grâce à sa transformée de FOURIER
![]()
![]() u, v
u, v![]() .
.
![]() x, y
x, y![]() ait été échantillonnée avec des pas
ait été échantillonnée avec des pas ![]() x et
x et ![]() y constants.
Soit
fr
y constants.
Soit
fr![]() x, y
x, y![]() l'image reconstruite définie par
l'image reconstruite définie par 
![]() x, y
x, y![]() correspond au plus proche échantillon
connu. L'image reconstruite peut donc être vue comme une image en
escaliers. Elle peut également s'écrire
correspond au plus proche échantillon
connu. L'image reconstruite peut donc être vue comme une image en
escaliers. Elle peut également s'écrire 
![]() x, y
x, y![]() soit
à bande limitée (ce qui extrêmement rare en pratique) et échantillonnée
correctement (en concordance avec le théorème de SHANNON).
soit
à bande limitée (ce qui extrêmement rare en pratique) et échantillonnée
correctement (en concordance avec le théorème de SHANNON).