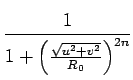3.2.3 Filtres passe-bas

Un exemple commun de filtre passe-bas est le filtre passe-bas de BUTTERWORTH d'ordre n défini par la fonction de transfert suivante

$$\mathcal {H} \left(\vphantom{u,v}\right. \left.\vphantom{u,v}\right) {\frac{{1}}{{1+\left(\frac{\sqrt{u^{2}+v^{2}}}{R_{0}}\right)^{2n}}}}$$ (3.11)

On remarque ici que toutes les composantes fréquentielles, hormis l'origine, subissent une atténuation d'autant plus grande que le couple $\left(\vphantom{u,v}\right.$u, v$\left.\vphantom{u,v}\right)$ est éloigné de l'origine. Plus l'ordre n du filtre est élevé, plus l'atténuation des hautes fréquences est importante. La transmittance du filtre passe-bas de BUTTERWORTH pour n = 1 est représentée à la figure 3.5.

Figure 3.5: Transmittance du filtre passe-bas de BUTTERWORTH pour n = 1.

 

Figure 3.6: Image filtrée par un filtre passe-bas de BUTTERWORTH d'ordre 1 (f_c = 30).

(a) Image filtrée	(b) Spectre de l'image filtrée

L'effet d'un filtrage passe-bas est généralement néfaste pour les contours. La figure 3.7 montre une image originale et trois versions filtrées par un filtre de plus en plus sélectif. On y observe une atténuation progressive du bruit ainsi qu'une dégradation croissante des contours.

Figure 3.7: Effet d'un filtrage passe-bas sur une image.