| h(x, y) = g(x', y')e2 |
(3.13) |
Les filtres de GABOR ou filtres gaussiens constituent une classe particulière des filtres linéaires; ce sont des filtres orientés. Ces filtres ont une réponse impulsionnelle de la forme:
| h(x, y) = g(x', y')e2 |
(3.13) |
La transformée de FOURIER correspondante est:
| (3.14) |

|
![]() (u, v) est une gaussienne passe-bande de rapport d'axes
1/
(u, v) est une gaussienne passe-bande de rapport d'axes
1/![]() , tournée d'un angle
, tournée d'un angle ![]() , centrée en
F =
, centrée en
F = ![]() et d'orientation
et d'orientation
![]() = tan-1(V/U). On prend habituellement
= tan-1(V/U). On prend habituellement
![]() =
= ![]() .
.
Présentés ainsi, les filtres de GABOR jouissent de quatre
degrés de liberté qui permettent d'extraire une partie de l'information
spectrale de l'image. Il s'agit du rapport d'axes ![]() , du facteur
d'excentricité
, du facteur
d'excentricité ![]() des gaussiennes dans les deux plans, et de
la translation imposée par (U, V) ou (F,
des gaussiennes dans les deux plans, et de
la translation imposée par (U, V) ou (F,![]() ) dans le domaine
des fréquences.
) dans le domaine
des fréquences.
Les filtres de GABOR sont une classe particulière des filtres linéaires, ce sont des filtres orientés. Ils permettent de mettre en évidence des textures ainsi que des zones homogènes d'une image. Grâce à la forme gaussienne des filtres, les enveloppes des images filtrées apportent une information spectrale locale en chaque pixel. De plus, elles renseignent sur le contenu énergétique de l'image dans la direction du filtre choisi.
L'usage des filtres gaussiens se justifie par le fait qu'ils minimisent
un certain type d'incertitude. Considérons une
fonction
f![]() x, y
x, y![]() et sa transformée de FOURIER
et sa transformée de FOURIER
![]()
![]() u, v
u, v![]() . Selon la propriété d'homothétie de
la transformée de FOURIER, nous avons
. Selon la propriété d'homothétie de
la transformée de FOURIER, nous avons
| f |
(3.15) |
Plus une fonction est localisée dans le domaine spatial, moins elle l'est dans le domaine fréquentiel, et vice-versa. Cette propriété est similaire au principe d'incertitude d'HEISENBERG.
On peut définir les extensions effectives d'une fonction
f![]() x, y
x, y![]() ,
centrée en
,
centrée en
![]() x0, y0
x0, y0![]() et dont la transformée de FOURIER
est centrée en
et dont la transformée de FOURIER
est centrée en
![]() u0, v0
u0, v0![]() , dans le domaine spatial
, dans le domaine spatial
![]() x et
x et ![]() y, et fréquentiel
y, et fréquentiel ![]() u et
u et ![]() v
respectivement, en considérant la racine carrée de la variance de
la distribution d'énergie de cette fonction. Les variances valent
v
respectivement, en considérant la racine carrée de la variance de
la distribution d'énergie de cette fonction. Les variances valent
Le principe d'incertitude montre que (cf. DAUGMAN [3])
On peut montrer que ce produit d'incertitude est minimisé par les fonctions de GABOR qui sont des fonctions gaussiennes modulées
En utilisant les définitions des extensions effectives, on pourrait montrer que
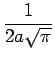 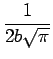 |
(3.23) |
| (3.24) |
Dès lors, quelles que soient les valeurs de a et de b, les fonctions de GABOR minimisent l'incertitude 3.20.
La fonction de GABOR (équation 3.21)
est le produit d'une gaussienne elliptique de rapport b/a dont
le centre est situé en
![]() x0, y0
x0, y0![]() par une exponentielle
complexe représentant une modulation par une fréquence radiale
par une exponentielle
complexe représentant une modulation par une fréquence radiale
![]() dont l'orientation est
tan-1
dont l'orientation est
tan-1![]() v0/u0
v0/u0![]() . La représentation
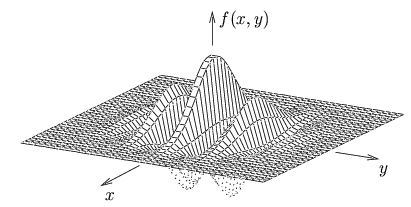
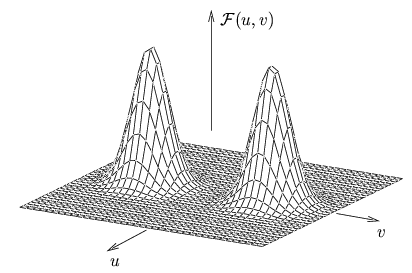
de la partie réelle d'une fonction de GABOR est donnée à
la figure 3.12 tandis que sa transformée
de FOURIER est représentée à la figure 3.13.
. La représentation
de la partie réelle d'une fonction de GABOR est donnée à
la figure 3.12 tandis que sa transformée
de FOURIER est représentée à la figure 3.13.
|
|
Comme le montre la figure 3.13, les fonctions
de GABOR peuvent servir de filtres sélectifs, ne gardant
que les composantes fréquentielles de l'image situées dans un voisinage
centré en
![]() u0, v0
u0, v0![]() , la taille de ce voisinage étant
fixée par les valeurs de a et de b. Il est également possible
de faire subir une rotation aux fonctions de GABOR afin que
les axes principaux des ellipses ne coïncident plus avec les axes
u - v. Enfin, il est courant que l'on utilise un banc de filtres
de GABOR afin de mettre en évidence différentes textures
et zones homogènes qui sont présentes dans l'image.
, la taille de ce voisinage étant
fixée par les valeurs de a et de b. Il est également possible
de faire subir une rotation aux fonctions de GABOR afin que
les axes principaux des ellipses ne coïncident plus avec les axes
u - v. Enfin, il est courant que l'on utilise un banc de filtres
de GABOR afin de mettre en évidence différentes textures
et zones homogènes qui sont présentes dans l'image.