3.3.3 Approche déterministe ou aléatoire?

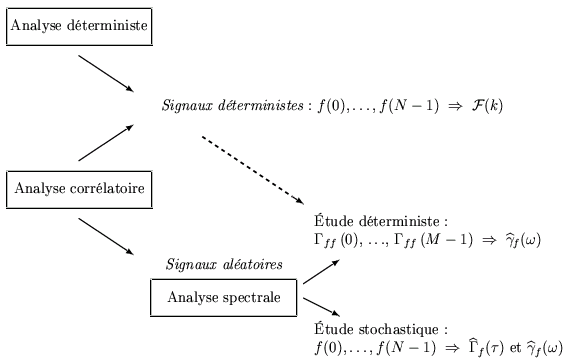
En toute généralité les échantillons f (n) peuvent provenir d'un signal déterministe ou aléatoire. La théorie du traitement du signal rattache quantité de méthodes et d'algorithmes à chacune de ces hypothèses. Pour y voir plus clair, nous avons dressé un tableau récapitulatif à la figure 3.16.

Figure 3.16: Récapitulatif des techniques de caractérisation des signaux.

 

L'analyse déterministe veille à tirer des renseignements de la séquence f (n): étude de la moyenne, recherche d'une fréquence dominante dans la transformée de Fourier, conditionnement du signal pour éviter le repli de spectre, ...

L'analyse corrélatoire, terme emprunté à DUVAUT [6], introduit un outil de comparaison entre deux signaux décalés, la fonction d'autocorrélation $\Gamma_{{ff}}^{}$$\left(\vphantom{\tau}\right.$$\tau$$\left.\vphantom{\tau}\right)$. Si ceux-ci sont déterministes, la forme de la fonction $\Gamma_{{ff}}^{}$$\left(\vphantom{\tau}\right.$$\tau$$\left.\vphantom{\tau}\right)$ reste voisine des variations de f (n) ; elle reproduit par exemple les mêmes périodicités. S'ils sont aléatoires, l'aspect de la fonction varie à chaque réalisation et dès lors ne constitue qu'une indication. Ce n'est que lorsque les signaux sont stationnaires (faiblement au moins), que l'analyse corrélatoire prend son sens. À ce stade, l'analyse spectrale complète l'étude par une signature spectrale de la fonction d'autocorrélation ; il s'agit de sa transformée de Fourier appelée densité spectrale, notée $\gamma_{{f}}^{}$($\omega$), et son usage, assujetti à la même contrainte de stationnarité, indique la répartition fréquentielle de l'énergie.

Selon PAPOULIS [24], l'analyse spectrale, c'est-à-dire l'analyse corrélatoire appliquée à des signaux aléatoires stationnaires, se découpe en deux catégories dépendant de la connaissance de la fonction d'autocorrélation. Supposons que soient connus M échantillons $\Gamma_{{ff}}^{}$$\left(\vphantom{0}\right.$ 0$\left.\vphantom{0}\right)$, ...,$\Gamma_{{ff}}^{}$$\left(\vphantom{M-1}\right.$M - 1$\left.\vphantom{M-1}\right)$. L'étude s'apparente à une étude déterministe où certains échantillons de $\Gamma_{{ff}}^{}$$\left(\vphantom{\tau}\right.$$\tau$$\left.\vphantom{\tau}\right)$ sont manquants. Pour estimer la densité spectrale $\tilde{{\gamma}}_{{f}}^{}$($\omega$), il faut tenir compte de cette apodisation soit en gérant l'influence de la fenêtre (méthodes non paramétriques), soit en identifiant le spectre à celui d'un modèle de données (méthodes paramétriques), ce qui conduit à une extrapolation de $\Gamma_{{ff}}^{}$$\left(\vphantom{\tau}\right.$$\tau$$\left.\vphantom{\tau}\right)$ au-delà du segment connu. Souvent on utilise des modèles autorégressifs ou à moyenne mobile. Parfois le signal est supposé à bande spectrale limitée ou alors l'objectif consiste à maximiser l'entropie de la densité spectrale. Il arrive aussi qu'aucun échantillon de la fonction d'autocorrélation ne soit à disposition. Ce cas, repris sous le terme d'une étude stochastique, nécessite le calcul conjoint des estimées $\tilde{{\Gamma}}_{{ff}}^{}$($\tau$) et $\tilde{{\gamma}}_{{f}}^{}$($\omega$).

Ce survol des techniques spectrales suffit à comprendre la réelle difficulté de la sélection d'un modèle. Nous avons jugé préférable de restreindre le travail à une analyse déterministe. Pourquoi un tel choix?

1. La raison principale est la facilité de mise en oeuvre: le recours à l'analyse spectrale nécessite un complément de modélisation, or aucune méthode ne satisfait tous les points de vue (qualité de l'estimation, réduction du bruit, minimisation des biais, etc). Il ne faudrait pas en conclure que nous perdons tout bénéfice des méthodes propres à des signaux aléatoires. En effet, les méthodes s'appuient sur des algorithmes qui eux s'appliquent à toutes les analyses. Par exemple, l'extrapolation itérative d'une séquence, à bande étroite, de signaux déterministes ou de la fonction d'autocorrélation, peut se réaliser de la même manière.
2. Un autre argument justifiant notre choix est la mise en doute de l'hypothèse de stationnarité qui sous-tend les développements de l'analyse spectrale. HUNT [14] met sa validité en cause dans le cas d'une image. Pour y remédier, il propose de stationnariser le signal, de le traiter et de revenir au signal de départ par inversion du processus de stationnarisation.
3. Enfin, si l'analyse spectrale achève une bonne discrimination de fréquences, elle remplit moins notre objectif de codage. De fait, les textures sont représentées par des échantillons de la transformée de Fourier du signal extrapolé et non de sa fonction d'autocorrélation. Une analyse corrélatoire devra donc se doubler d'un schéma pour convertir ces types d'information.

En conclusion, les développements théoriques repris dans ce chapitre dérivent d'une approche déterministe au problème d'extrapolation, quoique les algorithmes étudiés soient parfois repris par la littérature dans d'autres contextes, tel celui de l'analyse corrélatoire.