|
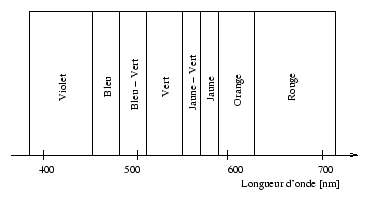
La lumière couvre une partie du spectre d'énergie électromagnétique. Un rayonnement électromagnétique est en général constitué d'un certain nombre de longueurs d'onde (ou fréquences) que les dispositifs dispersifs de séparer en un spectre. Le spectre est soit discret, soit continu.
Les longueurs d'onde du spectre visible s'étendent approximativement de 380 à 720 [nm]. Une source est caractérisée par (i) son rayonnement, mesurable dans un système de grandeur correspondant à l'action proprement visuelle, (ii) par le mélange des longueurs d'onde de cette énergie, mélange qui produit une sensation de couleur. La lumière est donc une distribution d'énergie émise à certaines fréquences ayant une certaine intensité.
Pour caractériser une couleur monochromatique,
il suffit de connaître sa longueur d'onde ![]() et la luminance
L, expression qualitative de la brillance énergétique. Dans ces
conditions, l'oeil se comporte donc comme un récepteur bivariant,
la connaissance de
et la luminance
L, expression qualitative de la brillance énergétique. Dans ces
conditions, l'oeil se comporte donc comme un récepteur bivariant,
la connaissance de ![]() et de celle de L étant nécessaires
et suffisantes pour caractériser l'impression visuelle créée.
et de celle de L étant nécessaires
et suffisantes pour caractériser l'impression visuelle créée.
Supposons maintenant une source constituée d'un certain nombre de radiations simples formant un spectre de raies ou un spectre continu avec une répartition énergétique donnée. La question qui se pose est le problème de la résultante, pour le récepteur visuel, de l'addition de l'ensemble de ces radiations. Des études psychovisuelles ont révélé les lois suivantes (cf. le livre de BUSER et d'IMBERT [1] pour les détails):
| L1 + L2 = Lb + Lr | (1.1) |
| (1.2) |
Une première possibilité de représenter une couleur consiste à estimer l'ensemble de ses composantes spectrales. En principe, il suffirait de filtrer le signal de couleur par une série de filtres à bande étroite et de mesurer l'intensité de chaque sortie filtrée. Le signal de couleur vaut alors
| (1.3) |
Une autre possibilité de représentation consiste à utiliser un espace de couleurs à k dimensions. Des expériences psychovisuelles d'égalisation (voir KUNT et al. [19]) ont montré qu'en combinant trois stimuli de longueur d'ondes particulières, il est possible de synthétiser presque toutes les couleurs existantes. Cette expérience peut s'effectuer à l'aide d'un système de reproduction de couleurs de type additif ou de type soustractif.
Choisissons trois radiations monochromatiques que nous qualifierons de primaires. Le problème sera de déterminer dans quelle mesure il est possible, à partir de ces trois couleurs, de reproduire une radiation colorée quelconque et selon quelles règles quantitatives. Dans le cas d'un mélange additif, l'expérience d'égalisation des couleurs se déroule par exemple de la manière suivante: trois couleurs primaires A, B et C sont, après pondération de de leur intensité respectivement par a, b et c, projetées sur écran noir avec un certain recouvrement comme l'illustre la figure 1.3.
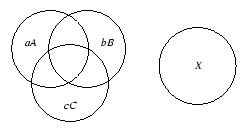
|
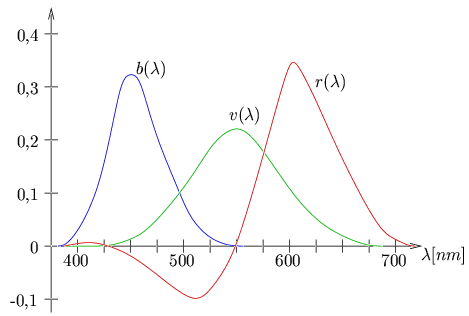
Pour des raisons de standardisation, la commission internationale de l'éclairage (CIE) a réalisé en 1931 l'expérience d'égalisation de couleur par mélange additif. Un système qui s'imposa presque naturellement était fondé sur les trois couleurs monochromatiques, rouge R (700 [nm]), vert V ( 546, 1 [nm]) et bleu B ( 435, 8 [nm]), ces deux dernières étant émises par l'arc au mercure (d'où leur choix). Ce fut le système RGB. On a ainsi déterminé pour ce système:
|
La figure 1.5 représente le diagramme chromatique-type dans le système RGB: chaque couleur primaire est placée au sommet d'un triangle isocèle rectangle; l'ensemble des couleurs monochromatiques s'aligne sur le contour du diagramme, dit lieu spectral, tandis qu'une radiation complexe se situe à l'intérieur du contour.
Pour être plus précis, les trois couleurs RGB définissent un triangle significatif de la perception visuelle. À condition de respecter les proportions, il est possible de moduler les composantes d'une intensité minimale à une intensité maximale. L'ensemble des couleurs représentables se situe donc à l'intérieur d'un pyramide telle que représentée à la figure 1.6.
À l'usage, il s'est avéré que ce système RGB présentait un certain nombre d'inconvénients (cf. [1]) du fait, en particulier que: (i) en raison du choix des primaires, l'une des coordonnées trichromatiques était toujours négative pour les radiations monochromatiques, (ii) on risquait d'attribuer aux couleurs primaires une signification physiologique qu'elles n'ont pas (puisque leur choix est arbitraire).
Afin de parer à ces inconvénients, la CIE a introduit, également en 1931, un autre espace de couleurs appelé XYZ. Les composantes X, Y et Z qui décrivent un stimulus sont liées aux composantes RGB par la relation matricielle suivante [19]
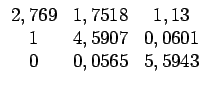 |
(1.4) |
En normalisant le tri-stimulus XYZ par rapport à X + Y + Z, on obtient
le système xyz. Une particularité intéressante de ce nouveau référentiel
est que seules deux variables, par exemple x et y, sont indépendantes.
Ces deux composantes sont appelées les composantes chromatiques
du stimulus. On a donc les relations
| x | = | 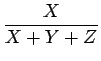 |
(1.5) |
| y | = | 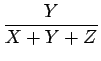 |
(1.6) |
| z | = | 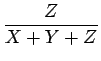 |
(1.7) |
| x + y + z | = | 1 | (1.8) |
Les couleurs monochromatiques sont représentées sur la partie non rectiligne du contour (comme un U retourné). Les couleurs qui résultent d'un mélange d'un mélange additif de certaines couleurs de base sont représentées à l'intérieur de la forme en U. Il existe aussi certains point particuliers, comme le point d'égale énergie qui correspond à une contribution égale des trois composantes de base X, Y et Z, ce qui correspond à x = y = 1/3. L'expérience d'égalisation des couleurs a montré qu'il suffisait de trois couleurs de base pour synthétiser la quasi-totalité des stimuli colorés. Comme le diagramme chromatique xy ne reprend que deux variables indépendantes, ce diagramme est une version réduite de l'espace à trois dimensions tel défini par le cube de la figure 1.8.
C'est dans ce genre d'espace que nous avons représenté les couleurs du diagramme chromatique approché à la figure 1.7; le diagramme tridimensionnel correspondant est illustré à la figure 1.9.
La dimension non représentée sur ce diagramme est celle de la luminance qui permet d'éclaircir ou d'assombrir une couleur en modulant son degré de noir. Par exemple, en modulant du minimum au maximum la luminance du point d'égale énergie, on passe du noir au blanc en passant par toutes les teintes de gris. Chaque couleur possède une luminance maximale dont la représentation graphique est fournie à la figure 1.10.
Le diagramme chromatique xy est donc le lieu des couleurs de chrominance (x, y) de luminosité maximale. En effet, un changement des proportions entre x et y conduirait automatiquement à la perception d'une autre couleur. Les deux variables de chrominance x et y peuvent se transformer en variables possédant une interprétation physique plus intuitive à savoir la teinte et la saturation. La notion de teinte (hue en anglais) est associée à la longueur d'onde, c'est-à-dire à la position le long du U retourné. La saturation exprime quant à elle le degré de blanc; elle est définie comme la distance entre le point d'égale énergie et la couleur à définir.
La figure 1.11 illustre la décomposition d'une image dans les trois canaux RGB et HSI.
La détermination des composantes RGB d'une onde s'opère par addition sur fond noir. L'arrière-plan est donc supposé absorbant pour toutes les couleurs. Un tel système n'est pas adéquat pour traiter l'impression sur feuille blanche car cette dernière réfléchit l'ensemble des couleurs. Pour l'impression, on a donc défini d'autres systèmes de couleurs, complémentaires au système RGB. Il s'agit par exemple du système Cyan, Magenta et Yellow (CMY), complémentaire du système RGB et dont la somme produit le noir1.1.
À côté du système RGB, couramment utilisé en infographie, il existe d'autres systèmes de couleurs tels les systèmes YIQ, YUV ou YCbCr. Ces systèmes de couleurs peuvent être calculés par transformation matricielle des composantes RGB auxquelles on a préalablement appliqué une correction gamma1.2.
Les standards de télévision analogiques (PAL, NTSC) définissent
chacun les positions de couleurs RGB dans le diagramme chromatique.
À cet égard, il est intéressant de remarquer que, contrairement
aux apparences, ces positions ne se situent pas sur le pourtour. Autrement
dit, les couleurs de base ne sont pas monochromatiques! Comme les
positions de ces systèmes ne coïncident pas, la totalité des couleurs
d'un système n'est pas représentable dans un autre système. D'autre
part, un téléviseur n'est pas réellement calibré à la fabrication
et son usage produit une usure. Cela nous amène à considérer avec
beaucoup de prudence la signification physique réelle d'une couleur
affichée par un téléviseur. On peut exprimer des réserves similaires
pour le cas des moniteurs utilisés dans le monde informatique. Pour
désigner une couleur en infographie, on utilise généralement une quantification
sur 8 bits par composante de couleurs. Les couleurs sont alors représentées
par un triplet de valeurs exprimées en hexadécimal, en décimal (cf.
table 1.1) ou en binaire.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
La représentation des valeurs d'une image nécessite 8 bits dans le cas d'une image monochrome et 3×8 = 24 dans le cas d'une image RGB. Pour réduire le nombre de bits dans le cas d'une image en couleurs, on réduit la taille de l'espace des couleurs en sous-échantillonnant l'espace RGB. Il est également possible de considérer les 256 valeurs d'une image comme les 256 indices d'un vecteur tridimensionnel reprenant les composantes RGB de couleurs. On parle alors de palette de couleurs ou de Color Look Up Table (CLUT). La figure 1.12 montre la palette de couleurs utilisées par le logiciel de navigation Netscape Navigator ainsi que la décomposition des couleurs dans les composantes RGB.
|
La figure 1.13 montre une image monochrome et une image obtenue en considérant une palette de couleurs aléatoires -on parle représentation en fausses couleurs car elles ne représentent pas des couleurs physiques.
|
La couleur d'un objet est significative de la réflectance de l'objet ainsi que de l'éclairage. Dès lors, à supposer qu'un onde lumineuse isochromatique (c'à-d. blanche) soit envoyée en direction de l'objet, sa surface absorbera certaines longueurs d'onde et en réfléchira d'autres. On ne pourra donc jamais définir la couleur que comme la couleur liée à la longueur d'onde dominante.
De plus, la réflexion peut être spéculaire (effet de miroir) ou être diffuse. L'infographie utilise abondamment ces techniques pour créer des effets d'ambiance. Un exemple, produit avec le logiciel BLENDER, est fourni à la figure 1.14.