Sous-sections
L'opération de dilatation, appelée dilation
en anglais, due à MINKOWSKI se définit de manière analogue.
En prenant le même élément structurant B, pour chaque position
z du centre de B la question est: l'ensemble Bz touche-t-il
X
(X  Bz
Bz 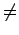
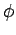 )? L'ensemble des points de
)? L'ensemble des points de
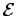 correspondant à une réponse positive forme le nouvel ensemble
X
correspondant à une réponse positive forme le nouvel ensemble
X 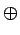
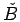 -l'ensemble
-l'ensemble 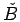 s'obtient par réflexion de l'ensemble
B autour de l'origine- dont la frontière est le lieu des centres
géométriques de Bz lorsque Bz touche X.
s'obtient par réflexion de l'ensemble
B autour de l'origine- dont la frontière est le lieu des centres
géométriques de Bz lorsque Bz touche X.
Le principe de la dilatation, à savoir l'union des translatés de X
par les éléments de B, est illustré à la figure 4.5.
Figure 4.5:
Illustration de la définition algébrique de la dilatation.
|
|
La figure 4.6 montre la dilatation par un
disque du même ensemble X que celui traité lors de l'érosion. Dans
cet exemple, les deux composantes connexes 4.1 sont réunies dans le dilaté; tout comme l'érosion, la dilation ne
préserve pas la connexité.
Figure 4.6:
Dilatation de X par un disque B.
|
|
Propriété 14
[Dualité] La transformation de
dilatation n'est pas indépendante de l'opération d'érosion. Éroder
X revient à dilater son complémentaire Xc. Les opérations
de dilatation et d'érosion sont donc deux opérations duales
par rapport à la complémentation:
Avec nos définitions d'érosion et de dilatation, la présence du symétrique
de B est inévitable. C'est pour l'éviter que certains auteurs adoptent
parfois une autre définition de l'érosion.
L'exploitation de cette propriété permet bien souvent de transposer
le travail fait pour une érosion à celui d'une dilatation et vice-versa.
De plus, la pratique favorise l'emploi d'éléments symétriques, d'où
découle une forme simplifiée du principe de dualité par complémentation.
Les opérations d'érosion et de dilatation vérifient les principes
des transformations morphologiques idéales:
- l'érosion et la dilatation sont invariantes en translation: de fait,
il revient au même de translater un ensemble X puis de l'éroder,
que de l'éroder puis de translater l'image transformée:
Xz
 B = (X
B = (X  B)z.
De même,
Xz
B)z.
De même,
Xz 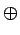 B = (X
B = (X 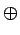 B)z;
B)z;
- l'érosion et la dilatation sont compatibles avec les homothéties:
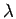 X
X 
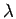 B =
B = 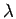 (X
(X  B) et
B) et
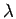 X
X 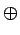
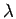 B =
B = 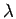 (X
(X 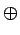 B);
B);
- l'érosion et la dilatation vérifient la condition de connaissance
locale pour B borné;
- nous admettrons sans démonstration que l'érosion et la dilatation
sont des transformations continues. Pour une démonstration rigoureuse,
le lecteur consultera par exemple l'ouvrage de SERRA [32].
Dans la pratique, la mathématique morphologique s'utilise sur des
images discrétisées; la discrétisation escamote considérablement les
problèmes de continuité.
Les deux opérations morphologiques jouissent aussi de propriétés algébriques:
- l'érosion et la dilatation sont des opérations croissantes:
si
X
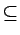 Y, alors
(X
Y, alors
(X  B)
B) 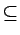 (Y
(Y  B) et
(X
B) et
(X 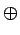 B)
B) 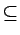 (Y
(Y 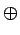 B);
B);
- si l'élément structurant contient l'origine, l'érosion est une opération
anti-extensive alors que la dilatation
est extensive, c.-à-d.
X
 B
B 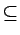 X
et
X
X
et
X 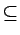 X
X 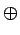 B.
B.
Notes
- ...4.1
- Un ensemble X est connexe si
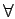 x1, x2
x1, x2 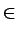 X
, il existe un chemin reliant x1 à x2 totalement inclus
dans X.
X
, il existe un chemin reliant x1 à x2 totalement inclus
dans X.
Marc Van Droogenbroeck. Tous droits réservés.
2003-09-30
![]() Bz
Bz ![]()
![]() )? L'ensemble des points de
)? L'ensemble des points de
![]() correspondant à une réponse positive forme le nouvel ensemble
X
correspondant à une réponse positive forme le nouvel ensemble
X ![]()
![]() -l'ensemble
-l'ensemble ![]() s'obtient par réflexion de l'ensemble
B autour de l'origine- dont la frontière est le lieu des centres
géométriques de Bz lorsque Bz touche X.
s'obtient par réflexion de l'ensemble
B autour de l'origine- dont la frontière est le lieu des centres
géométriques de Bz lorsque Bz touche X.