Table des matières of 4.3.5 Propriétés générales

Pour décrire des réalisations logicielles ou matérielles, il est utile de mettre en lumière quelques propriétés supplémentaires (les démonstrations manquantes sont disponibles dans l'article d'HARALICK [10]):

Propriété 17 La dilatation est commutative et associative

X $\displaystyle \oplus$ B = B $\displaystyle \oplus$ X

(4.12)

(X $\displaystyle \oplus$ Y) $\displaystyle \oplus$ C = X $\displaystyle \oplus$ (Y $\displaystyle \oplus$ C)

(4.13)

4.3.5.1 Remarques concernant l'implémentation des opérations morphologiques élémentaires

Dans la pratique, X et B sont des objets très différents puisque B est l'élément structurant. La dilatation par un carré de taille 3×3 est une opération aisée à réaliser dans une architecture actuelle. La propriété d'associativité est fondamentale pour ce qui est du nombre d'opérations à réaliser lorsque X est analysé par (B $\oplus$ C). Soit N une dimension caractéristique de B et C (largeur ou hauteur), une application brutale de la dilatation de X par B $\oplus$ C nécessite N² opérations alors que la succession de la dilatation X $\oplus$ B suivie de la dilatation par C requiert 2N opérations. Cependant l'intérêt reste restreint pour des architectures qui effectuent la dilatation par accès aléatoire à tous les points du voisinage.

Des efforts de recherche constants sont entrepris pour réduire le nombre d'opérations nécessaires. Par exemple, VINCENT [42] a mis au point un algorithme souple et performant pour déterminer les dilatations et érosions d'images binaires avec des éléments structurants quelconques. La première étape consiste en un suivi de contours de l'image et en leur codage sous forme de boucles. Dans un second temps, l'élément structurant représenté par une structure de données appropriée, est efficacement propagé le long de ces boucles. D'autres références [38] proposent un algorithme de complexité N et un autre algorithme indépendant de la taille de l'élément structurant sur base de la manipulation d'un histogramme local. Ces algorithmes permettent aussi d'effectuer une ouverture en une seule passe. ZHUANG [44] propose une méthode utilisable pour des éléments structurants convexes (c'est ce qu'on appelle des ``STEINER'') du type B = (B₁ $\oplus$ B₂). En fait, la plupart des propriétés citées ci-après induisent un algorithme particulier permettant une certaine optimisation des opérations morphologiques. Tantôt, l'élément structurant est décomposé par dilatation, tantôt par intersection ou encore par union.

Propriété 18 La dilatation distribue l'union

( $\displaystyle \bigcup_{{j}}^{}$ X_j) $\displaystyle \oplus$ B = $\displaystyle \bigcup_{{j}}^{}$ (X_j $\displaystyle \oplus$ B)

(4.14)

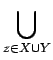(X $\displaystyle \cup$ Y) $\displaystyle \oplus$ B = $\displaystyle \bigcup_{{z\in X\cup Y}}^{}$ B_z = ( $\displaystyle \bigcup_{{z\in X}}^{}$ B_z) $\displaystyle \cup$ ( $\displaystyle \bigcup_{{z\in Y}}^{}$ B_z) = (X $\displaystyle \oplus$ B) $\displaystyle \cup$ (Y $\displaystyle \oplus$ B)

(4.15)

Par commutativité, X $\oplus$ (B $\cup$ C) = (X $\oplus$ B) $\cup$ (Y $\oplus$ C). Cette égalité est importante; elle permet la décomposition d'un élément structurant en une union d'éléments structurants, offrant ainsi une alternative dans l'évaluation du coût d'une réalisation.

Propriété 19 L'érosion est distributive par rapport à l'intersection

( $\displaystyle \bigcap_{{j}}^{}$ X_j) $\displaystyle \ominus$ B = $\displaystyle \bigcap_{{j}}^{}$ (X_j $\displaystyle \ominus$ B)

(4.16)

( $\displaystyle \bigcap_{{j}}^{}$ X_j) $\displaystyle \ominus$ B = $\displaystyle \bigcap_{{b\in B}}^{}$ $\displaystyle \bigcap_{{j}}^{}$ X_j-b = $\displaystyle \bigcap_{{j}}^{}$ $\displaystyle \bigcap_{{b\in B}}^{}$ X_j-b = $\displaystyle \bigcap_{{j}}^{}$ (X_j $\displaystyle \ominus$ B)

(4.17)

La relation suivante est régulièrement utilisée pour réduire le temps de calcul d'une érosion par un grand élément structurant. C'est la relation de chaîne , appelée chain rule.

Propriété 20

X $\displaystyle \ominus$ (B $\displaystyle \oplus$ C) = (X $\displaystyle \ominus$ B) $\displaystyle \ominus$ C

(4.18)

Cette relation a son importance car elle permet d'effectuer des érosions d'éléments structurants de grande taille et décomposables en une dilatation de deux plus petits éléments -par exemple, un carré est équivalent à une dilatation d'un segment horizontal par un segment vertical- par deux érosions successives de taille réduite.

Propriété 21

X $\displaystyle \oplus$ B = (X $\displaystyle \oplus$ B)oB = (X $\displaystyle \bullet$ B) $\displaystyle \oplus$ B (4.21)

Propriété 22 L'ouverture et la fermeture ne dépendent pas de l'origine de l'élément structurant, comme le suggérait l'interprétation de ces opérations. Soit z $\in$ $\mathcal {E}$

X`o`B_z	=	X`o`B	(4.22)
X $\displaystyle \bullet$ B_z	=	X $\displaystyle \bullet$ B	(4.23)

4.3.5.2 Un problème pratique: la gestion du bord dans les réalisations

Si l'invariance en translation découle des définitions des opérations morphologiques, la pratique contredit sa véracité parce que le bord de champ limite la connaissance de l'objet à un certain domaine. Une translation de l'image entraîne une perte irréversible d'information. Deux attitudes, correspondant à des hypothèses physiques sur l'extérieur du domaine d'observation et illustrées à la figure 4.8, sont possibles: soit l'objet s'étend au-delà du masque (hypothèse 1), soit on suppose que, physiquement, il n'y a rien en dehors du masque (hypothèse 2).

**Figure 4.8:** Deux hypothèses physiques pour traiter les objets qui touchent le bord de l'image.

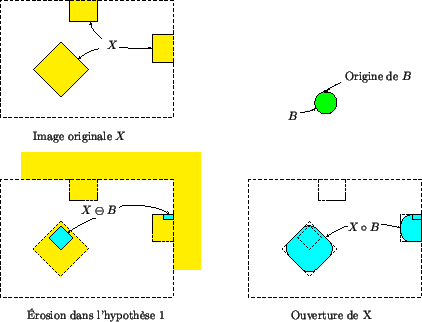
Dans la seconde situation, les traitements morphologiques ne posent pas de problème car on dispose de toute l'information nécessaire. Il en va autrement pour la première hypothèse. Soit à effectuer, par exemple, une érosion. On a beau admettre que l'objet s'étende en dehors de l'image, cela ne signifie pas pour autant que l'on puisse délimiter cette zone d'extension. Le pis-aller habituel consiste à ajouter à X tous les points situés à l'extérieur de l'image lors du calcul de l'érodé. Cela modifie le résultat de l'érosion, comme le montrent les érosions par un disque centré, représentées à la figure 4.9. Par dualité, le calcul de la dilatation s'effectue en supposant que les points extérieurs n'appartiennent pas à l'ensemble.

**Figure 4.9:** Comparaison de l'érosion de X, composé de deux losanges, pour les deux hypothèses physiques.

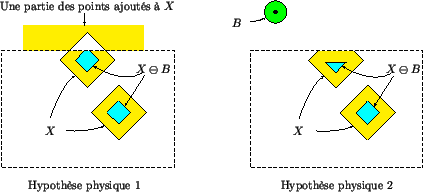
Contrairement aux apparences, ceci n'est pas suffisant pour traiter correctement une ouverture dans le cas de l'hypothèse 1. Prenons l'exemple de l'ouverture de X par le disque B décentré, dessiné à la figure 4.10. Malgré la présence d'un bord lors du calcul de l'érosion, le rectangle du haut ne crée aucune contribution dans X $\ominus$ B, et donc dans l'ouvert, alors qu'une même surface située à droite subsistera en partie dans l'ouvert. De plus, déplacer l'origine de B vers l'extrémité droite du disque inverse le résultat. Il n'est pourtant pas logique que le résultat dépende à ce point de la position de l'origine, surtout après avoir énoncé la propriété d'indépendance de cette position dans le résultat de l'ouverture.

**Figure 4.10:** Pour illustrer que l'ouverture n'est pas unique malgré l'ajout d'un bord lors de l'érosion.

Soit M le masque d'observation, celui fixé par le bord de l'image. Comme remède, nous proposons une ``définition pratique'' de l'ouverture, à savoir

XoB = $\displaystyle \bigcup_{{p\in\mathbb{R}^{2}}}^{}$ ([(X $\displaystyle \cup$ M^c) $\displaystyle \ominus$ B_p] $\displaystyle \oplus$ B_p) $\displaystyle \cap$ M (4.24)

Pour la plupart des éléments structurants, quelques positions p suffiront à obtenir la totalité de l'ouvert. Dans le pire des cas, il faudra les prendre en nombre égal au périmètre de B.

(X $\displaystyle \ominus$ B) $\displaystyle \ominus$ C	=	$\displaystyle \bigcap_{{c\in C}}^{}$ ( $\displaystyle \bigcap_{{b\in B}}^{}$ X_-b)_-c = $\displaystyle \bigcap_{{c\in C}}^{}$ ( $\displaystyle \bigcap_{{b\in B}}^{}$ X_-(b+c)) = $\displaystyle \bigcap_{{c\in C}}^{}$ $\displaystyle \bigcap_{{b\in B}}^{}$ X_-(b+c)	(4.19)
	=	X $\displaystyle \ominus$ (B $\displaystyle \oplus$ C)	(4.20)