Une dilatation goédésique fait toujours intervenir deux images. La
première image est le dilaté par un élément structurant élémentaire
isotropique adapté à la trame; il s'agit d'un carré de trois pixels
de large pour une trame carrée et d'un hexagone dans une trame hexagonale.
Quant à la seconde image, elle limite l'extension de la dilatation
de la première.
Suite à l'apparition de l'intersection dans la définition,
DY(1)(X)
est toujours inclus ou égal à Y. On dit aussi que Y sert de
masque géodésique. La figure 4.11
illustre le principe de la dilatation géodésique de taille 1 sur
un ensemble dans une trame hexagonale.
Définition 26
La dilatation géodésique de taille n de l'ensemble X
conditionnellement à Y, notée
DY(n)(X), est définie comme
une succession du dilaté géodésique de taille 1
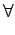 X X 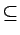 Y, DY(n)(X) = Y, DY(n)(X) =  (X))) (X))) |
(4.32) |
où B est l'élément le plus simple adapté à la trame.
Il est important de remarquer que
DY(n)(X) n'est pas toujours
égal à l'ensemble obtenu en intersectant X dilaté par l'élément
structurant B de taille n avec Y. Prenons le cas d'un ensemble
Y formé de plusieurs composantes connexes et de X réduit à une
composante de Y. Suite à la définition de la dilatation géodésique,
DY(n)(X) = X alors que le résultat de l'intersection après
plusieurs dilatations pourra contenir des parties des autres composantes
connexes de Y.
Marc Van Droogenbroeck. Tous droits réservés.
2003-09-30
 (X)))
(X)))