Un filtre linéaire est constitué d'un opérateur, bien entendu linéaire et continu, mais aussi commutant avec les translations et ayant, dans certains cas, des propriétés d'idempotence (filtre passe-bande idéal, par exemple).
Dans une image, un objet placé au-devant de la scène occulte tous
ceux qui se trouvent derrière lui dans l'axe d'observation. Pour exprimer
cet aspect fondamental, on a nécessairement recours à la notion d'inclusion
qui remplace, dans l'univers visuel, la structure d'additivité qui
régit d'autres univers. Le filtrage morphologique constitue une alternative
au filtrage linéaire. Rappelons que les filtres morphologiques ne
possèdent aucune propriété de linéarité; supposons deux fonctions
de gris f (x) et g(x) et une transformation morphologique ![]() ,
on aura généralement:
,
on aura généralement:
![]() (f (x) + g(x))
(f (x) + g(x)) ![]()
![]() (f (x)) +
(f (x)) + ![]() (g(x))
(g(x))
Nous avons vu que les ouvertures morphologiques permettaient de lisser les objets d'une image binaire. D'où l'idée d'appliquer des filtrages sur des formes ou des images en niveaux de gris. Nous allons à présent enrichir la famille des filtres non-linéaires après avoir préalablement défini quelques propriétés algébriques.
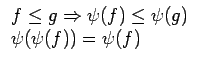 |
(5.5) |
| (5.6) | |||
| = | (5.7) | ||
| f | (5.8) |
La propriété de croissance dresse un fort parallélisme avec les filtres linéaires, surtout sous la forme suivante:
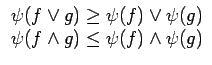 |
(5.9) |