En combinant les filtres déjà connus! Mais toutes les combinaisons
ne sont pas permises: par exemple, la composition de deux ouvertures
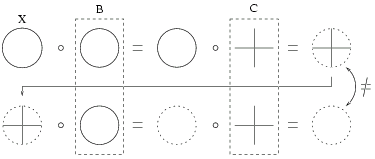
n'est ni une ouverture ni un filtre, comme le montre la figure 5.5.
Dans cet exemple, une nouvelle application donnera un ensemble vide
et la propriété d'idempotence ne sera pas satisfaite.
Figure 5.5:
La composition de deux ouvertures n'est pas forcément une ouverture.
|
|
De nouveaux filtres peuvent être obtenus à partir des ouvertures,
notées
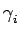 dans cette section, et des fermetures,
notées
dans cette section, et des fermetures,
notées 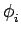 , par les deux règles simples que voici:
, par les deux règles simples que voici:
- le supremum d'ouvertures est une ouverture:
(
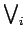
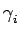 )
est une ouverture;
)
est une ouverture;
- l'infimum de deux fermetures est une fermeture:
(
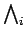
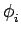 )
est une fermeture.
)
est une fermeture.
Certaines compositions de filtres permettent aussi d'obtenir des nouveaux
filtres. Soient 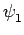 et
et 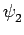 deux filtres tels que
deux filtres tels que
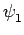
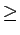 I
I 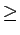
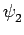 (par exemple,
(par exemple, 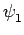 est une fermeture et
est une fermeture et 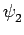 une ouverture).
Le théorème structurel définit quelles compositions sont des filtres
et établit l'ordre des opérateurs.
une ouverture).
Le théorème structurel définit quelles compositions sont des filtres
et établit l'ordre des opérateurs.
Marc Van Droogenbroeck. Tous droits réservés.
2003-09-30
![]() dans cette section, et des fermetures,
notées
dans cette section, et des fermetures,
notées ![]() , par les deux règles simples que voici:
, par les deux règles simples que voici: