Table des matières of 7.2.2 Modulation d'amplitude numérique cohérente

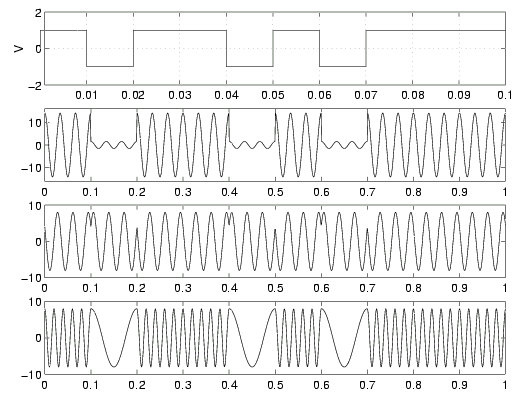
La modulation numérique d'amplitude porte le nom anglais d'Amplitude-Shift Keying (ASK) qui, dans le cas où un signal est nul, s'appelle on/off keying. Son principe est illustré, en même temps que celui de la modulation de phase et de fréquence, à la figure 7.1. Un signal modulant NRZ à deux états d'amplitude, A₀ et A₁, multiplie une porteuse. À supposer que les symboles successifs de la source soient indépendants entre eux, la séquence modulée peut être vue comme la somme de deux signaux modulés de type on/off keying. Pour construire chacun d'eux, il suffit de prendre un signal nul au droit des symboles de l'autre séquence.

s₀(t) = $\displaystyle \sum_{{k=-\infty}}^{{+\infty}}$ A_kRect_{[0, T_b]}(t - kT_b)cos(2 $\displaystyle \pi$ f_ct)

(7.2)

7.2.2.1 Occupation spectrale

Tout signal fini ayant un spectre infini et cette situation étant inacceptable pour les systèmes de transmission, le signal d'émission subira un filtrage préalable à la transmission. Encore faut-il être en mesure de déterminer les fréquences les plus significatives du signal à émettre.

Dans un premier temps, prenons une approche déterministe. Le cas le plus défavorable, c'est-à-dire celui qui fournira la fréquence significative la plus élevée, est celui où il y alternance continuelle entre les deux symboles dans le signal modulant m₀(t). Cela mène à un développement en série de FOURIER de la forme

m₀(t) = $\displaystyle {\frac{{A_{0}}}{{2}}}$ $\displaystyle \left[\vphantom{1+\frac{4}{\pi}\cos(2\pi(\frac{1}{2}f_{b})t)-\frac{4}{3\pi}\cos(2\pi(\frac{3}{2}f_{b})t)+\ldots}\right.$ 1 + $\displaystyle {\frac{{4}}{{\pi}}}$ cos(2 $\displaystyle \pi$ ( $\displaystyle {\frac{{1}}{{2}}}$ f_b)t) - $\displaystyle {\frac{{4}}{{3\pi}}}$ cos(2 $\displaystyle \pi$ ( $\displaystyle {\frac{{3}}{{2}}}$ f_b)t) +... $\displaystyle \left.\vphantom{1+\frac{4}{\pi}\cos(2\pi(\frac{1}{2}f_{b})t)-\frac{4}{3\pi}\cos(2\pi(\frac{3}{2}f_{b})t)+\ldots}\right]$

(7.3)

La composante continue vaut A₀/2 et on remarque la présence de raies spectrales aux multiples impairs de la moitié de la fréquence des bits, c'est-à-dire (2n + 1)f_b/2. Il n'y a pas de raie spectrale pour les multiples entiers de la cadence du flux binaire. Le spectre du signal modulé s₀(t) est obtenu par transposition du spectre initial à la fréquence de porteuse

s₀(t)	=	$\displaystyle {\frac{{A_{0}}}{{2}}}$ $\displaystyle \left[\vphantom{\cos(2\pi f_{c}t)+\frac{2}{\pi}\cos(2\pi(f_{c}+\frac{f_{b}}{2})t)+\frac{2}{\pi}\cos(2\pi(f_{c}-\frac{f_{b}}{2})t)}\right.$ cos(2 $\displaystyle \pi$ f_ct) + $\displaystyle {\frac{{2}}{{\pi}}}$ cos(2 $\displaystyle \pi$ (f_c + $\displaystyle {\frac{{f_{b}}}{{2}}}$ )t) + $\displaystyle {\frac{{2}}{{\pi}}}$ cos(2 $\displaystyle \pi$ (f_c - $\displaystyle {\frac{{f_{b}}}{{2}}}$ )t)
		$\displaystyle \left.\vphantom{-\frac{2}{3\pi}\cos(2\pi(f_{c}+\frac{3f_{b}}{2})t)-\frac{2}{3\pi}\cos(2\pi(f_{c}-\frac{3f_{b}}{2})t)+\ldots}\right.$ - $\displaystyle {\frac{{2}}{{3\pi}}}$ cos(2 $\displaystyle \pi$ (f_c + $\displaystyle {\frac{{3f_{b}}}{{2}}}$ )t) - $\displaystyle {\frac{{2}}{{3\pi}}}$ cos(2 $\displaystyle \pi$ (f_c - $\displaystyle {\frac{{3f_{b}}}{{2}}}$ )t) +... $\displaystyle \left.\vphantom{-\frac{2}{3\pi}\cos(2\pi(f_{c}+\frac{3f_{b}}{2})t)-\frac{2}{3\pi}\cos(2\pi(f_{c}-\frac{3f_{b}}{2})t)+\ldots}\right]$	(7.4)

Si, au lieu d'être régulière, la séquence d'entrée est aléatoire et les probabilités d'un 0 ou d'un 1 équiprobables, on peut raisonnablement penser que le spectre réel prolongera continûment le spectre discret obtenu pour la séquence régulière. D'un point de vue formel, la modélisation ne diffère en rien de la modélisation faite pour la transmission numérique en bande de base à condition de respecter la condition de cohérence 7.1.

On montre après calculs que la densité spectrale de puissance s'exprime comme la densité spectrale du signal modulant multipliée par la transformée de FOURIER de la porteuse (à un facteur 1/2 près), ce qui dans le cas présent donne

$\displaystyle \gamma$ (f )	=	$\displaystyle \left[\vphantom{p_{0}(1-p_{0})A_{0}^{2}T_{b}\left(\frac{\sin(\pi fT_{b})}{\pi fT_{b}}\right)^{2}+p_{0}^{2}A_{0}^{2}\delta(f)}\right.$ p₀(1 - p₀)A₀²T_b $\displaystyle \left(\vphantom{\frac{\sin(\pi fT_{b})}{\pi fT_{b}}}\right.$ $\displaystyle {\frac{{\sin(\pi fT_{b})}}{{\pi fT_{b}}}}$ $\displaystyle \left.\vphantom{\frac{\sin(\pi fT_{b})}{\pi fT_{b}}}\right)^{{2}}_{}$ + p₀²A₀² $\displaystyle \delta$ (f ) $\displaystyle \left.\vphantom{p_{0}(1-p_{0})A_{0}^{2}T_{b}\left(\frac{\sin(\pi fT_{b})}{\pi fT_{b}}\right)^{2}+p_{0}^{2}A_{0}^{2}\delta(f)}\right]$ $\displaystyle \otimes$ $\displaystyle {\frac{{\delta(f-f_{c})+\delta(f+f_{c})}}{{4}}}$	(7.5)
	=	$\displaystyle {\frac{{p_{0}(1-p_{0})A_{0}^{2}T_{b}}}{{4}}}$ $\displaystyle \left(\vphantom{\frac{\sin(\pi(f-f_{c})T_{b})}{\pi(f-f_{c})T_{b}}}\right.$ $\displaystyle {\frac{{\sin(\pi(f-f_{c})T_{b})}}{{\pi(f-f_{c})T_{b}}}}$ $\displaystyle \left.\vphantom{\frac{\sin(\pi(f-f_{c})T_{b})}{\pi(f-f_{c})T_{b}}}\right)^{{2}}_{}$ + $\displaystyle {\frac{{p_{0}(1-p_{0})A_{0}^{2}T_{b}}}{{4}}}$ $\displaystyle \left(\vphantom{\frac{\sin(\pi(f+f_{c})T_{b})}{\pi(f+f_{c})T_{b}}}\right.$ $\displaystyle {\frac{{\sin(\pi(f+f_{c})T_{b})}}{{\pi(f+f_{c})T_{b}}}}$ $\displaystyle \left.\vphantom{\frac{\sin(\pi(f+f_{c})T_{b})}{\pi(f+f_{c})T_{b}}}\right)^{{2}}_{}$
		+ $\displaystyle {\frac{{p_{0}^{2}A_{0}^{2}}}{{4}}}$ $\displaystyle \delta$ (f - f_c) + $\displaystyle {\frac{{p_{0}^{2}A_{0}^{2}}}{{4}}}$ $\displaystyle \delta$ (f + f_c)	(7.6)

Comme on pouvait le pressentir, le spectre se compose d'une raie à la fréquence porteuse flanquée, de part et d'autre, du spectre du signal modulant. Le spectre du signal ASK s'obtient en additionnant les spectres respectifs de s₀(t) et de s₁(t) en tenant compte du fait que p₀ + p₁ = 1, ce qui ne change rien à l'occupation spectrale.

L'expression rigoureuse du spectre du signal ASK (relation 7.6) confirme l'étendue infinie du spectre. L'usage veut que le spectre filtré contienne au moins la fréquence critique telle que déterminée précédemment, à savoir f_b/2. On choisira typiquement une fréquence de coupure de 0, 6f_b à 0, 75f_b ce qui conduit à une bande passante du signal modulé de 1, 2f_b à 1, 5f_b.

7.2.2.2 Démodulation cohérente

Le schéma d'un démodulateur ASK cohérent ne diffère pas du schéma utilisé pour la bande de base; il comporte un filtre adapté, suivi d'un organe de décision. Quelques éléments relatifs à la chaîne de modulation et de démodulation sont illustrés aux figures 7.2 et 7.3.

On y voit respectivement le signal modulé, le signal modulé bruité, la sortie du filtre adapté et le diagramme de l'oeil.

La forte sensibilité de la modulation ASK à des phénomènes de distorsion d'amplitude la rend inadéquate pour des environnements fortement bruités; on lui préfère alors une modulation angulaire.