|
L'analyse de la modulation analogique et de ses performances donnent l'impression que l'objectif poursuivi est de transmettre à tout instant la valeur exacte du signal porteur d'information. C'est en effet à quoi tendent les techniques de modulation classique par une porteuse sinusoïdale, telles qu'utilisées dans la majorité des systèmes de télécommunications actuels. Pourtant, dès les années 1940, des savants comme NYQUIST, SHANNON ou WIENER établirent le cadre mathématique théorique des télécommunications. C'est grâce à eux que l'on pu prendre conscience du caractère illusoire de cette prétention.
Les signaux porteurs d'information sont généralement à spectre limité -c'est à tout le moins l'hypothèse que nous avons formulée précédemment. Dans les systèmes de télécommunications analogiques, on tire usage de cette propriété en effectuant un multiplexage en fréquence. Mais il est possible d'adopter une autre approche. En effet, le signal étant à spectre limité, sa valeur ne peut varier infiniment vite et il suffit sans doute de sélectionner des échantillons représentatifs du signal à une condition appropriée. Le théorème de SHANNON montre que si la fréquence d'échantillonnage est supérieure à une certaine limite, cela suffit pour que le récepteur soit à même de reconstituer parfaitement le signal de départ.
D'autre part, que l'on transmette le message de façon continue ou échantillonnée, il est illusoire d'en donner la valeur exacte. Comme les transducteurs d'émission et de réception n'ont pas un comportement parfait et que le canal de transmission lui-même introduit du bruit et des distorsions, il est superflu de vouloir restituer la valeur instantanée exacte du message. Aussi, si du moins cela apporte un avantage, peut-on coder cette valeur en un nombre comportant une quantité limitée de chiffres significatifs: c'est une quantification de la valeur instantanée. Ce procédé se marie parfaitement avec une technique d'échantillonnage.
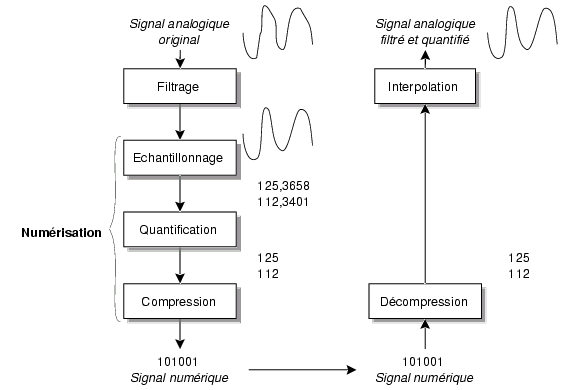
On retrouve les opérations d'échantillonnage et de quantification déjà évoquées à la figure 6.1 qui montre une chaîne de numérisation complète.
La partie gauche couvre les étapes de conversion de l'analogique en signaux numériques. Ces derniers se prêtent tout naturellement à une opération de compression qui, dans les systèmes modernes de télécommunications, est toujours présente. Pour reconstituer le signal analogique, les signaux numériques sont traités par un interpolateur représenté à droite.
La numérisation du signal ne garantit pas la correspondance entre le signal original et le signal issu de l'interpolateur. En effet, certaines étapes de la chaîne de numérisation introduisent une erreur sur le signal. La maîtrise de cette erreur est alors la clé d'une numérisation réussie.