Table des matières of 6.3 Modulation PAM

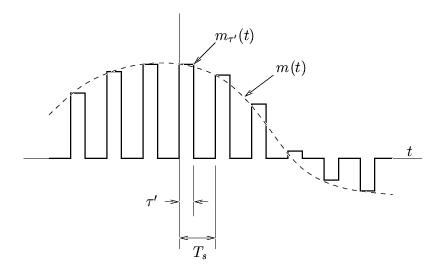
La forme la plus simple de modulation d'impulsions analogiques est la modulation de l'amplitude des impulsions (Pulse Amplitude Modulation, PAM). Comme son nom l'indique, elle consiste à moduler l'amplitude d'un train d'impulsions équidistantes, en fonction des valeurs des échantillons d'un signal analogique (cf. figure 6.7). Remarquons que l'usage du mot modulation prend ici un sens particulier car il n'est nullement question de moduler les paramètres d'une porteuse mais bien d'affecter le signal de départ.

Que les impulsions soient de forme rectangulaire ou autre importe peu pour le principe de la méthode, ce qui ne signifie nullement que la forme n'ait pas de d'influence sur l'occupation spectrale ou sur les performances, que du contraire!

On construit le signal PAM m(t) en maintenant le signal à une valeur constante. Ce signal diffère de g(t) car m(t) reste constant et égal à la valeur de l'échantillon pendant un certain temps $\tau{^\prime}$ .

On peut considérer que m(t) résulte non plus de la multiplication de la fonction échantillonnée par un rectangle de largeur $\tau{^\prime}$ mais de la convolution:

m(t) = p(t) $\displaystyle \otimes$ $\displaystyle \left[\vphantom{g(t)\sum_{n=-\infty}^{+\infty}\delta(t-nT_{s})}\right.$ g(t) $\displaystyle \sum_{{n=-\infty}}^{{+\infty}}$ $\displaystyle \delta$ (t - nT_s) $\displaystyle \left.\vphantom{g(t)\sum_{n=-\infty}^{+\infty}\delta(t-nT_{s})}\right]$

(6.17)

$\displaystyle \mathcal {M}$ (f )	=	$\displaystyle \mathcal {P}$ (f ) $\displaystyle \left[\vphantom{\mathcal{G}(f)\otimes \left(\frac{1}{T_{s}}\sum_{n=-\infty}^{+\infty}\delta(f-nf_{s})\right)}\right.$ $\displaystyle \mathcal {G}$ (f ) $\displaystyle \otimes$ $\displaystyle \left(\vphantom{\frac{1}{T_{s}}\sum_{n=-\infty}^{+\infty}\delta(f-nf_{s})}\right.$ $\displaystyle {\frac{{1}}{{T_{s}}}}$ $\displaystyle \sum_{{n=-\infty}}^{{+\infty}}$ $\displaystyle \delta$ (f - nf_s) $\displaystyle \left.\vphantom{\frac{1}{T_{s}}\sum_{n=-\infty}^{+\infty}\delta(f-nf_{s})}\right)$ $\displaystyle \left.\vphantom{\mathcal{G}(f)\otimes \left(\frac{1}{T_{s}}\sum_{n=-\infty}^{+\infty}\delta(f-nf_{s})\right)}\right]$	(6.18)
	=	$\displaystyle \mathcal {P}$ (f ) $\displaystyle {\frac{{1}}{{T_{s}}}}$ $\displaystyle \sum_{{n=-\infty}}^{{+\infty}}$ $\displaystyle \mathcal {G}$ (f - nf_s)	(6.19)
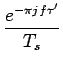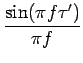	=	$\displaystyle {\frac{{e^{-\pi jf\tau'}}}{{T_{s}}}}$ $\displaystyle {\frac{{\sin(\pi f\tau')}}{{\pi f}}}$ $\displaystyle \sum_{{n=-\infty}}^{{+\infty}}$ $\displaystyle \mathcal {G}$ (f - nf_s)	(6.20)

Cette expression diffère de 6.16 en ce que chaque spectre répété de la fonction m(t) subit une déformation due au facteur du sinus cardinal. Un filtrage passe-bas du signal restitue donc m(t) avec une déformation importante si $\tau{^\prime}$ est appréciable par rapport à T_s, mais ceci peut se corriger par un filtre correcteur.

Une chaîne de conditionnement qui se limite à la mise en forme de signaux en vue d'un traitement effectif comprend, dans une version relativement complète, une conversion analogique-numérique suivie, selon les besoins, d'un filtre numérique destiné à adapter partiellement les propriétés fréquentielles au traitement ultérieur. Comme nous l'avons vu, la chaîne de conversion se voit précédée d'un filtre analogique passe-bas qui ajuste la bande passante du signal en fonction de la fréquence caractéristique de l'échantillonnage.