|
L'étude du bruit de quantification est très importante non seulement pour le choix du nombre de niveaux de quantification, mais aussi de la représentation de ceux-ci. Ce qui importe en effet n'est pas le niveau de bruit de quantification mais plutôt le rapport des puissances moyennes à bruit de quantification.
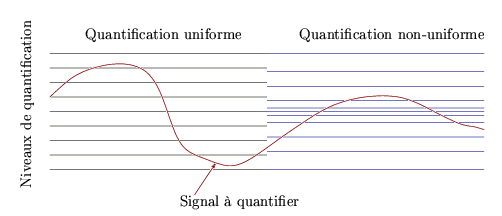
Or, on sait que le puissance moyenne d'un signal de télécommunications peut varier dans une large mesure. Par exemple, pour un signal téléphonique, la puissance moyenne peut varier de quelques 20 à 30 [dB] selon la distance de l'abonné, l'état de son appareil et selon qu'il parle plus ou moins fort. Avec une quantification linéaire, le niveau de bruit reste constant, quelle que soit la puissance du signal; par conséquent, les signaux faibles auront un rapport signal à bruit de quantification défavorable. Si l'on veut uniformiser le rapport signal à bruit de quantification, il y a donc lieu de diminuer le pas de quantification aux faibles niveaux, c'est-à-dire d'adopter une quantification non linéaire, comme illustrée à la figure 6.13. En fait, il faut proportionner la densité des niveaux de quantification à la densité de probabilité fM(m) du signal.
Ceci peut se faire de deux manières: soit en utilisant un codeur à niveaux non uniformément répartis, soit en utilisant un codeur linéaire précédé d'un circuit non linéaire ayant une caractéristique en forme de S, et dont le but est d'uniformiser la densité de probabilité. Un tel circuit non linéaire est appelé compresseur. Le circuit complémentaire utilisé à la réception s'appelle un extenseur.
Pour une répartition donnée des niveaux de quantification, le rapport
signal à bruit de quantification dépend de la densité de probabilité
du signal m ainsi que de sa répartition de puissance dans le spectre.
Soit le signal modulant m la réalisation d'une variable aléatoire
M de moyenne nulle. Si l'entrée n'a pas une moyenne nulle, rien
n'empêche de soustraire la valeur moyenne avant quantification et
de rajouter cette valeur au moment de reconstruire les échantillons.
Un quantificateur ![]() (.) est une application qui envoie la variable
aléatoire M d'amplitude continue sur une variable aléatoire discrète
V
(.) est une application qui envoie la variable
aléatoire M d'amplitude continue sur une variable aléatoire discrète
V
| (6.25) |
| q = v - m | (6.26) |
ou encore
| Q = V - M | (6.27) |
Lorsque le signal d'entrée M est de moyenne nulle et que le quantificateur est symétrique, il advient que la sortie du quantificateur est également de moyenne nulle. Il suffit dès lors de déterminer la valeur quadratique moyenne de l'erreur de quantification pour en déduire le rapport signal à bruit.
En tenant compte des moyennes nulles, les valeurs quadratiques moyennes du signal et de bruit de quantification s'obtiennent par les formules
| (6.28) |
| (6.29) |
Prenons le cas d'un signal m défini sur l'intervalle
[- mmax, mmax].
Supposons qu'il s'agisse d'un quantificateur linéaire de la forme
représentée à la figure 6.12(b). Le pas
de ce quantificateur, noté ![]() , vaut
, vaut
s'il y a L niveaux possibles. La linéarité du quantificateur
permet de définir les bornes de l'erreur:
- ![]() /2
/2 ![]() q
q ![]()
![]() /2.
Pour un pas de quantification suffisamment petit, ce qui signifie
que le nombre de niveaux de quantification est grand, on peut admettre
que l'erreur de quantification Q a une densité de probabilité uniforme.
Moyennant cette hypothèse, la densité de probabilité de la variable
Q s'écrit
/2.
Pour un pas de quantification suffisamment petit, ce qui signifie
que le nombre de niveaux de quantification est grand, on peut admettre
que l'erreur de quantification Q a une densité de probabilité uniforme.
Moyennant cette hypothèse, la densité de probabilité de la variable
Q s'écrit
fQ(q) = 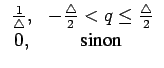 |
(6.31) |
Ajoutons que pour valider cette hypothèse, il est impératif que le signal m n'amène pas le quantificateur en saturation. On calcule alors la valeur de l'erreur quadratique moyenne
| (6.32) |
| (6.33) |
On peut traduire cette valeur en nombre de bits car c'est en effet sous une forme binaire que l'on transmet généralement les valeurs des indices k. Soit R le nombre de bits utilisés par échantillon. Le nombre de niveaux s'exprime comme
| L = 2R | (6.34) |
| R = log2L | (6.35) |
La substitution de cette valeur dans l'équation 6.30 mène à
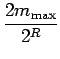 |
(6.36) |
| (6.37) |
Soit
![]() la puissance moyenne du message m(t). Le rapport
signal à bruit6.3 de quantification
la puissance moyenne du message m(t). Le rapport
signal à bruit6.3 de quantification
![]() /
/![]() est égal à
est égal à
| = | (6.38) | ||
| = | 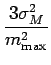 |
(6.39) |
L'ajout d'un bit supplémentaire augmente le rapport signal à bruit
de 6 [dB] puisqu'en décibels, le rapport signal à bruit vaut
| 10 log10 |
= | 10 log103 + 20 log10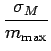 |
(6.40) |
| = | 4, 77 + 20 log10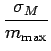 |
(6.41) |
L'ajout d'un bit élargit malheureusement aussi la bande nécessaire au signal. Toutefois, le compromis entre le rapport signal à bruit et la bande passante est plus avantageux que dans le cas de la modulation PPM, à condition de présumer qu'un système PPM soit jugé sur base du rapport signal à bruit et que le PCM le soit sur base du bruit de quantification.
Exemple: signal modulant sinusoïdal.
Prenons le cas d'un signal modulant sinusoïdal d'amplitude
Am que l'on veut quantifier sur toute sa dynamique. Pour une
résistance valant
1 [![]() ], la puissance vaut
Am2/2.
La plage de quantification s'étend de - Am à Am. Dès lors,
], la puissance vaut
Am2/2.
La plage de quantification s'étend de - Am à Am. Dès lors,
| 10 log10 |
(6.42) |
Pour des signaux modulants dont la densité de probabilité n'est pas aussi uniforme mais prend la forme d'une gaussienne par exemple, la quantification linéaire ne permet plus d'obtenir un bon rapport signal à bruit; celui-ci peut être amélioré en optant pour une quantification non linéaire. En téléphonie, on a adopté pour l'Europe une loi de codage non linéaire dite loi A; elle correspond à la courbe de compression de la figure 6.14(b).
La loi de codage normalisée par l'ITU est la loi A = 87, 6 approchée par 13 segments linéaire 8 bits, dans lequel le premier bit donne le signe, les trois suivants déterminent le segment et les quatre derniers fixent la position sur le segment. Cette courbe est particulièrement adaptée au signal téléphonique. Pour le codage d'autres signaux, dans une application bien particulière, il y aura lieu d'étudier la courbe de compression optimale.
Quant à la loi A, elle est définie comme
| v| = 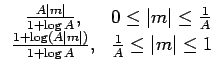 |
(6.43) |
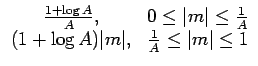 |
(6.44) |
Aux États-Unis, on utilise la loi ![]() dont l'expression analytique
est
dont l'expression analytique
est
| v| = 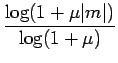 |
(6.45) |
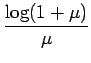 (1 + (1 + |
(6.46) |