x(t) = 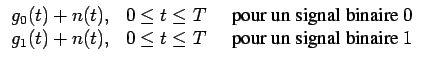 |
(7.94) |
Le signal reçu durant l'intervalle de temps T est
x(t) = 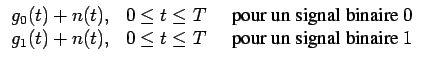 |
(7.94) |
Pour notre étude, considérons un signal NRZ, g0(t) = - V et g1(t) = + V.
Comme in fine le récepteur doit estimer quel signal a été reçu, il peut y avoir deux types d'erreur au moment de prendre une décision
Supposons que l'on ait transmis un symbole 0, autrement dit le
signal
g0(t) = - V pour
0 ![]() t
t ![]() Tb. Le signal reçu au
récepteur est alors
Tb. Le signal reçu au
récepteur est alors
| x(t) = - V + n(t) 0 |
(7.95) |
Dès lors, la sortie du filtre adapté ou corrélateur est
| y(t) | = | (7.96) | |
| = | (7.97) | ||
| = | (7.98) |
| y[Tb] | = | (7.99) | |
| = | kV2Tb - kV |
(7.100) |
| y[Tb] = - V + |
(7.101) |
Remarquons qu'il s'agit de la réalisation d'une variable aléatoire Y échantillonnée au temps t = Tb. Moyennant l'hypothèse d'un bruit additif blanc et gaussien n(t), la variable aléatoire Y jouit des caractéristiques suivantes:
| (7.106) |
Après substitution de cette valeur dans l'équation 7.105,
| = | (7.107) | ||
| = | (7.108) |
Et donc, la fonction de densité de probabilité de la variable aléatoire Y après transmission du symbole 0 vaut
fY(y| 0) = 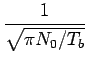 e- e- |
(7.109) |
Soit Pe0 la probabilité d'erreur conditionnelle tenant compte
de l'émission du symbole 0. En l'absence de bruit, la sortie du
filtre adapté fourni - V au temps d'échantillonnage t = Tb.
La situation est tout autre en présence de bruit. En effet, la réalisation
y(t) prend des valeurs tantôt supérieure, tantôt inférieure à - V.
À la limite, le bruit est tel que le signal se rapproche de la valeur
+ V relative au symbole 1, ce qu'il faut éviter. Si l'on définit
un seuil ![]() de décision situé entre - V et + V, il y aura
erreur sur le symbole 0 si la variable aléatoire dépasse la valeur
de ce seuil. Formellement, on écrit
de décision situé entre - V et + V, il y aura
erreur sur le symbole 0 si la variable aléatoire dépasse la valeur
de ce seuil. Formellement, on écrit
| Pe0 | = | p(y > |
(7.110) |
| = | (7.111) | ||
| = | 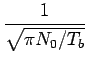 |
(7.112) |
Pour poursuivre, il faut fixer la valeur du seuil ![]() . Une
telle détermination se fonde sur la probabilité a priori des symboles
0 et 1, notées respectivement p0 et p1. En prenant
des probabilités égales telles que
p0 + p1 = 1,
. Une
telle détermination se fonde sur la probabilité a priori des symboles
0 et 1, notées respectivement p0 et p1. En prenant
des probabilités égales telles que
p0 + p1 = 1,
| p0 = p1 = |
(7.113) |
Dans le cas que nous traitons, les valeurs de crête des deux symboles sont équidistantes par rapport à l'origine le long de l'axe y. Il est dès lors logique de prendre
| (7.114) |
Cela nous permet de poursuivre le calcul de la probabilité conditionnelle; Pe0 devient
Pe0 = 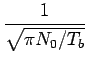 |
(7.115) |
Après le changement de variable
z = ![]() ,
on obtient
,
on obtient
Pe0 = 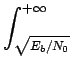 e-z2dz e-z2dz |
(7.116) |
![[*]](crossref.gif) )
)
| Eb = V2Tb | (7.117) |
Il est pratique d'introduire la fonction d'erreur complémentaire; elle est définie par
| erfc(u) = |
(7.118) |
Grâce à cette fonction, on obtient
Pe0 = 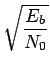 |
(7.119) |
La densité de probabilité fY(y| 0) et la probabilité d'erreur Pe0 sont représentées à la figure 7.8(a).
Supposons à présent que ce soit le signal g1(t) qui ait été envoyé. Un raisonnement similaire au précédent conduit rapidement à
fY(y| 1) = 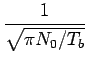 e- e- |
(7.120) |
On note par Pe1 la probabilité d'erreur conditionnelle après
émission du symbole 1. Son expression est
| Pe1 | = | p(y < |
(7.121) |
| = | (7.122) | ||
| = | 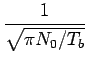 |
(7.123) |
En opérant le changement de variable
- z = ![]() ,
on remarque que
Pe0 = Pe1.
,
on remarque que
Pe0 = Pe1.
Les deux densités de probabilité sont représentées à la figure 7.9.
Pour déterminer la probabilité d'erreur au récepteur, on note que les deux types d'erreur énoncés précédemment sont exclusifs. On définit une probabilité d'erreur moyenne au récepteur Pe en pondérant les erreurs respectives par les probabilités a priori des signaux à l'émetteur
| Pe = p0Pe0 + p1Pe1 | (7.124) |
Dans notre cas, on en déduit la valeur suivante
Pe = 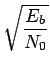 |
(7.125) |
Cette grandeur est généralement appelée taux d'erreur sur bit ou Bit Error Rate (BER).
Le taux d'erreur moyen d'un système PCM à deux états opposés dépend donc exclusivement du rapport entre l'énergie transmise par bit et la densité spectrale de bruit; la courbe est dessinée à la figure 7.10.
Comme il n'est pas possible d'agir sur la valeur de la puissance de bruit N0, diminuer la probabilité d'erreur ne pourra se faire que par l'augmentation de Eb. Puisque Eb = V2Tb, il faudrait donc augmenter V -du moins quand ce degré de liberté existe- ou ralentir la cadence d'émission.
En pratique, on recourt à une autre technique, en l'occurrence à celle des codes détecteurs ou correcteurs d'erreur qui diminue le taux d'erreur mais qui présente l'inconvénient d'élargir la bande de base à même débit utile d'information.