Sous-sections

3.3.2 Analyse de la modulation de fréquence analogique

3.3.2.1 Remarque préliminaire

L'analyse spectrale d'un signal modulé est évidemment très importante, car elle permet de déterminer la bande passante requise. Cette analyse était simple dans le cas de la modulation d'amplitude en raison de la propriété de linéarité dont elle jouit. En effet, soient s1(t) et s2(t) deux signaux modulés en amplitude créés à partir des signaux modulants m1(t) et m2(t) sur une même porteuse. Une combinaison linéaire des signaux modulés s'exprime comme

as1(t) + bs2(t) = aAc(1 + kam1(t))cos(2$\displaystyle \pi$fct) + bAc(1 + kam2(t))cos(2$\displaystyle \pi$fct)  
  = Ac(a + b + ka(am1(t) + bm2(t))cos(2$\displaystyle \pi$fct) (3.59)

Il s'agit donc bien d'une modulation en amplitude par la même combinaison linéaire des signaux modulants. C'est de là que vient la simplicité de l'analyse spectrale pour la modulation d'amplitude; celle-ci se ramène à des translations du spectre sur l'axe des fréquences.

La modulation angulaire ne possède pas une telle simplicité. En particulier, il est impossible de faire l'analyse spectrale en général. Seule est théoriquement modélisable l'application de la modulation angulaire à des signaux modulants typiques et simples, dont le cas de la cosinusoïde pure. Il faudra donc extrapoler, avec les réserves de circonstance quant à l'interprétation subséquente, le résultat acquis pour des signaux simples.

Le signal simple choisi pour cette étude est le signal modulant

m(t) = Amcos(2$\displaystyle \pi$fmt) (3.60)

correspondant à un ton simple dans le cas d'un signal sonore, pour lequel on dispose des outils mathématiques. Tant l'amplitude que la fréquence de ce signal sont des paramètres dans l'étude.

3.3.2.2 Modulation par une cosinusoïde

Il convient d'abord d'établir quelques équations valables pour les divers cas de modulation angulaire analogique et de bien saisir comment évoluent les caractéristiques du signal modulé en fonction des paramètres Am et fm du signal modulant m(t) = Amcos(2$ \pi$fmt). Par définition, la fréquence instantanée du signal modulé vaut

fi(t) = fc + kfAmcos(2$\displaystyle \pi$fmt) (3.61)
  = fc + $\displaystyle \triangle$f cos(2$\displaystyle \pi$fmt) (3.62)

où $ \triangle$f = kfAm est l'excursion ou déviation de fréquence. On voit que l'excursion de fréquence est proportionnelle à l'amplitude du signal modulant mais qu'elle ne dépend pas de sa fréquence.

Quant à la phase instantanée, l'application de l'équation 3.57 fournit

$\displaystyle \phi_{{i}}^{}$(t) = 2$\displaystyle \pi$fct + $\displaystyle {\frac{{\triangle f}}{{f_{m}}}}$sin(2$\displaystyle \pi$fmt) (3.63)

Cela entraîne une valeur d'indice de modulation qui est

$\displaystyle \beta$ = $\displaystyle {\frac{{\triangle f}}{{f_{m}}}}$ (3.64)

D'un point de vue physique, l'indice de modulation $ \beta$ représente l'écart angulaire maximum par rapport à l'angle de la porteuse; $ \beta$ s'exprime en radians.

La phase instantanée d'une porteuse modulée en fréquence par un signal modulant cosinusoïdal s'exprime dès lors sous la forme

$\displaystyle \phi_{{i}}^{}$(t) = 2$\displaystyle \pi$fct + $\displaystyle \beta$sin(2$\displaystyle \pi$fmt) (3.65)

On peut voir le cosinus de la porteuse comme la projection d'un rayon qui tourne le long du cercle trigonométrique (voir figure 3.18). La modulation implique des oscillations de la position du rayon autour d'une position déterminée par la vitesse de rotation angulaire 2$ \pi$fc; l'amplitude des oscillations est déterminée par l'indice de modulation.

Figure 3.18: Interprétation de la modulation de fréquence.
3203  

3.3.2.3 Analyse spectrale

Examinons à présent le spectre du signal FM tel qu'il résulte de l'application d'un signal modulant cosinusoïdal

s(t) = Accos(2$\displaystyle \pi$fct + $\displaystyle \beta$sin(2$\displaystyle \pi$fmt)) (3.66)

On peut toujours développer l'expression du signal modulé

s(t) = Accos(2$\displaystyle \pi$fct)cos($\displaystyle \beta$sin(2$\displaystyle \pi$fmt)) - Acsin(2$\displaystyle \pi$fct)sin($\displaystyle \beta$sin(2$\displaystyle \pi$fmt)) (3.67)

Pour calculer le spectre du signal s(t), on recourt à la formule suivante [8, page 987]

ej$\scriptstyle \beta$sin$\scriptstyle \psi$ = J0($\displaystyle \beta$) + 2$\displaystyle \sum_{{k=1}}^{{+\infty}}$jkJk($\displaystyle \beta$)cos$\displaystyle \left(\vphantom{k\left(\psi-\frac{\pi}{2}\right)}\right.$k$\displaystyle \left(\vphantom{\psi-\frac{\pi}{2}}\right.$$\displaystyle \psi$ - $\displaystyle {\frac{{\pi}}{{2}}}$$\displaystyle \left.\vphantom{\psi-\frac{\pi}{2}}\right)$$\displaystyle \left.\vphantom{k\left(\psi-\frac{\pi}{2}\right)}\right)$ (3.68)

ce qui peut encore s'écrire
cos($\displaystyle \beta$sin$\displaystyle \psi$) = J0($\displaystyle \beta$) + 2J2($\displaystyle \beta$)cos(2$\displaystyle \psi$) + 2J4($\displaystyle \beta$)cos(4$\displaystyle \psi$) +... (3.69)
sin($\displaystyle \beta$sin$\displaystyle \psi$) = 2J1($\displaystyle \beta$)sin$\displaystyle \psi$ +2J3($\displaystyle \beta$)sin(3$\displaystyle \psi$) +... (3.70)

où Jn($ \beta$) sont les fonctions de BESSEL de première espèce. La figure 3.19 représente la valeur des fonctions de BESSEL de première espèce.

Figure 3.19: Fonctions de BESSEL du premier ordre.
3247  

Sachant en plus que les fonctions de BESSEL possèdent les propriétés J2i($ \beta$) = J-2i($ \beta$) et J2i+1($ \beta$) = - J-(2i+1)($ \beta$), on peut réécrire le signal modulé sous la forme

s(t) = Ac$\displaystyle \sum_{{n=-\infty}}^{{+\infty}}$Jn($\displaystyle \beta$)cos(2$\displaystyle \pi$(fc + nfm)t) (3.71)

La transformée de FOURIER de ce signal fait apparaître un nombre infini de paires de raies aux fréquences fc + nfm de part et d'autre de la porteuse et ayant des amplitudes AcJn($ \beta$).

$\displaystyle \mathcal {S}$(f )= $\displaystyle {\frac{{A_{c}}}{{2}}}$$\displaystyle \sum_{{n=-\infty}}^{{+\infty}}$Jn($\displaystyle \beta$)[$\displaystyle \delta$(f - fc - nfm) + $\displaystyle \delta$(f + fc + nfm)] (3.72)

Alors que la position des raies latérales est régie par la fréquence du signal modulant, l'amplitude dépend de l'indice de modulation qui lui fait intervenir la fréquence fm et l'excursion maximale de fréquence $ \triangle$f.

On comprend bien l'expression du spectre en analysant les figures 3.20 et 3.21.

Figure 3.20: Spectre d'un signal FM (fm = 1, $ \beta$ variable).
3289  

La première montre l'évolution des valeurs absolues des amplitudes des 8 premières fréquences autour de la porteuse (cette dernière est indicée par 0); les amplitudes sont normalisées à 1 pour la facilité de la comparaison.

Figure 3.21: Spectre d'un signal FM ( $ \triangle$f = 1, $ \beta$ variable).
3298  

Pour poursuivre l'étude, distinguons deux cas en fonction de la valeur choisie pour l'indice de modulation $ \beta$:

  1. Modulation FM à faible indice ou modulation à bande étroite, pour laquelle $ \beta$ est petit par rapport à 1 radian.
  2. Modulation FM à grand indice ou modulation à large bande. Dans ce cas, $ \beta$ est largement supérieur à 1 radian.

3.3.2.4 Modulation FM à faible indice

La connaissance de l'allure des fonctions de BESSEL permet de simplifier l'expression du signal modulé. En effet, on peut montrer que, pour de faibles valeurs d'indice de modulation, les fonctions de BESSEL prennent les valeurs suivantes

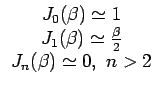$\displaystyle \left\{\vphantom{ \begin{array}{c} J_{0}(\beta)\simeq1\\ J_{1}(\beta)\simeq\frac{\beta}{2}\\ J_{n}(\beta)\simeq0,\,\, n>2\end{array}}\right.$$\displaystyle \begin{array}{c} J_{0}(\beta)\simeq1\\ J_{1}(\beta)\simeq\frac{\beta}{2}\\ J_{n}(\beta)\simeq0,\,\, n>2\end{array}$ (3.73)

Autrement dit, seules les deux premières fonctions ont une valeur significative pour une modulation à faible indice. On en déduit que le signal modulé vaut

s(t) $\displaystyle \simeq$ Accos(2$\displaystyle \pi$fct) + $\displaystyle {\frac{{1}}{{2}}}$$\displaystyle \beta$Ac$\displaystyle \left[\vphantom{\cos(2\pi(f_{c}+f_{m})t)-\cos(2\pi(f_{c}-f_{m})t)}\right.$cos(2$\displaystyle \pi$(fc + fm)t) - cos(2$\displaystyle \pi$(fc - fm)t)$\displaystyle \left.\vphantom{\cos(2\pi(f_{c}+f_{m})t)-\cos(2\pi(f_{c}-f_{m})t)}\right]$ (3.74)

Ce résultat est quelque peu semblable à ce que fournirait le développement d'une modulation d'amplitude par un signal cosinusoïdal, à savoir

s(t)AM = Accos(2$\displaystyle \pi$fct) + $\displaystyle {\frac{{1}}{{2}}}$kaAc$\displaystyle \left[\vphantom{\cos(2\pi(f_{c}+f_{m})t)+\cos(2\pi(f_{c}-f_{m})t)}\right.$cos(2$\displaystyle \pi$(fc + fm)t) + cos(2$\displaystyle \pi$(fc - fm)t)$\displaystyle \left.\vphantom{\cos(2\pi(f_{c}+f_{m})t)+\cos(2\pi(f_{c}-f_{m})t)}\right]$ (3.75)

La différence entre une modulation de fréquence à faible indice et une modulation d'amplitude par un signal cosinusoïdal se remarque au niveau du signe du dernier terme. La bande passante nécessaire est, par contre, identique.

3.3.2.5 Modulation FM à grand indice

Dans le cas d'une modulation de fréquence à grand indice, la détermination de la bande passante est plus délicate. Il existe néanmoins une propriété intéressante relative à la puissance et la distribution des valeurs relatives des termes du spectre. En effet, quelle que soit la valeur de l'indice de modulation, la puissance du signal modulé vaut invariablement P = $ {\frac{{1}}{{2}}}$Ac2. On remarquera d'autre part que $ \sum_{{n=-\infty}}^{{+\infty}}$Jn2($ \beta$) = 1, d'où l'on peut déduire

P = $\displaystyle {\frac{{1}}{{2}}}$Ac2$\displaystyle \sum_{{n=-\infty}}^{{+\infty}}$Jn2($\displaystyle \beta$) (3.76)

La somme des énergies des raies est donc constante et égale à la puissance du signal. Un étalement du spectre implique dès lors une diminution globale des amplitudes des raies. Parfois même, la porteuse disparaîtra pour certains choix de valeur pour l'indice de modulation3.4.


Notes

... modulation3.4
Supprimer totalement la porteuse est généralement déconseillé car cela complique l'acquisition de la porteuse à la réception; mais c'est néanmoins possible.
Marc Van Droogenbroeck. Tous droits réservés.
2005-03-11