Le développement précédent présuppose une durée particulière
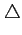 T
.
Il est intéressant d'examiner le comportement lorsque
m
T
.
Il est intéressant d'examiner le comportement lorsque
m 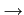 +
+ 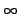 ,
c'est-à-dire lorsque
,
c'est-à-dire lorsque
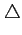 T
T 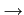 0
.
0
.
La densité de probabilité du dénombrement (relation 8.10)
peut s'écrire sous la forme suivante, pour
n = 0, 1, ..., m
,
| fDm(n) |
= |
Cmn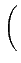 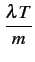 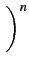  1 - 1 - 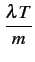 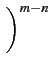 |
(8.11) |
| |
= |
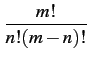  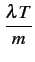 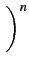  1 - 1 - 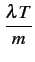 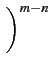 |
(8.12) |
| |
= |
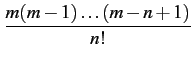 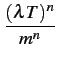  1 - 1 - 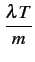 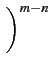 |
(8.13) |
| |
= |
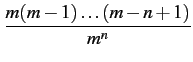 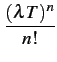  1 - 1 - 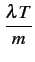 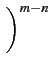 |
(8.14) |
Le premier facteur de ce produit contient n
termes au numérateur
et également n
termes au dénominateur. De plus, à mesure que
m 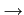 +
+ 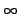 ,
chaque rapport de type
,
chaque rapport de type
 tend vers 1
. Dès lors,
tend vers 1
. Dès lors,
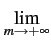 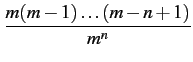 = 1 = 1 |
(8.15) |
Le second facteur ne dépend pas de m
. Quant au troisième
terme, il vaut
et donc
Dès lors,
qui n'est autre que la variable aléatoire de POISSON
de paramètre
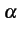 =
= 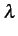 T
. Étant donné que l'on à fait tendre
m
vers l'infini, l'indice de la variable aléatoire Dm
n'a
plus de raison d'être; nous écrirons donc D
.
T
. Étant donné que l'on à fait tendre
m
vers l'infini, l'indice de la variable aléatoire Dm
n'a
plus de raison d'être; nous écrirons donc D
.
Définition 28
[Variable aléatoire de POISSON]
On appelle variable aléatoire
de POISSON une variable aléatoire D
discrète dont
la densité de probabilité est
fD(n) = 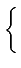 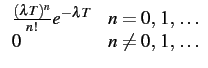 |
(8.19) |
Elle représente donc ici la probabilité d'avoir n
tentatives d'appels
pendant la durée T
.
La loi de POISSON fait intervenir un taux moyen d'occurrences
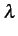 et un intervalle de temps d'observation T
; ces dénominations
sont justifiées par le théorème suivant (on définit
et un intervalle de temps d'observation T
; ces dénominations
sont justifiées par le théorème suivant (on définit
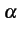 =
= 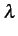 T
):
T
):
Théorème 29
[34, page 63] Soit à effectuer n
tirages. Pour chaque
tirage, la probabilité de l'événement pertinent est définie égale
à
 , où
, où 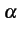 > 0
est une constante et n >
> 0
est une constante et n > 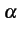 .
Soit une variable aléatoire Sn
qui dénombre les occurrences
d'événements pertinents pour n
tirages effectués. Lorsque
n
.
Soit une variable aléatoire Sn
qui dénombre les occurrences
d'événements pertinents pour n
tirages effectués. Lorsque
n 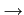 +
+ 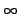 ,
la densité de probabilité de Sn
converge vers une loi de POISSON
de paramètre
,
la densité de probabilité de Sn
converge vers une loi de POISSON
de paramètre 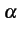 .
.
Démonstration.
Elle découle des développements précédents.
Théorème 30
L'espérance et la variance
d'une variable aléatoire de POISSON valent toutes deux 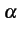
Démonstration.
Démontrons la relation 8.20.
Le terme i = 0
de la sommation vaut 0
. Après le changement de
variable i = j + 1
,
Le fait que la somme soit égale à 1
découle du fait que la fonction
de répartition de la loi de POISSON vaut 1
à l'infini (la
somme des probabilités définies par la variable aléatoire de POISSON
vaut 1
). La relation 8.21 se démontre
d'une manière identique.
Ainsi donc,
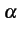 =
= 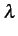 T
est égal à la valeur moyenne de la
loi de POISSON, d'où le fait que
T
est égal à la valeur moyenne de la
loi de POISSON, d'où le fait que
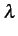 =
=  est la valeur moyenne du nombre d'occurrences par unité de temps;
on parle parfois d'intensité pour
est la valeur moyenne du nombre d'occurrences par unité de temps;
on parle parfois d'intensité pour 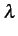 .
.
Question 31
Soit un taux moyen d'appels de 4
par minute. Quelle est la probabilité
P 5
d'avoir 5 appels ou plus pendant une minute?
5
d'avoir 5 appels ou plus pendant une minute?
Réponse
Par la variable de POISSON,
P 5 = 5 =  fD(i) = 1 - fD(i) = 1 -  fD(i) fD(i) |
(8.24) |
Comme
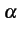 =
= 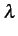 T = 4 x 1 = 4
,
T = 4 x 1 = 4
,
P 5 = 1 - 5 = 1 -  1 + 1 +  + +  + +  + + 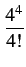  e-4 = 0, 37 e-4 = 0, 37 |
(8.25) |
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27
![]()
![]()
![]()
![]() 1 -
1 - ![]()
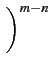
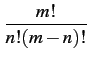
![]()
![]()
![]()
![]() 1 -
1 - ![]()
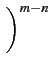
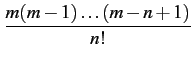
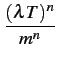
![]() 1 -
1 - ![]()
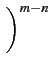
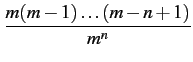
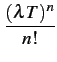
![]() 1 -
1 - ![]()
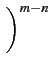
![]() +
+ ![]()
![]()
![]()
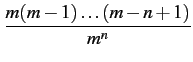 = 1
= 1![]() 1 -
1 - ![]()
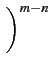 =
= 
![]()
 =
= ![]()
![]() 1 -
1 - ![]()
![]() = e-
= e-![]() T
T![]() fDm(n) =
fDm(n) = ![]()

![]() =
= ![]() T
T
![]()
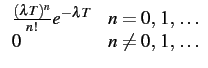
![]()
![]() =
= ![]() T
T
![]()
![]() > 0
> 0
![]()
![]() +
+ ![]()
![]()
![]() =
= ![]() ifD(i) =
ifD(i) = ![]() i
i![]() e-
e-![]()
![]() =
= ![]() (j + 1)
(j + 1) e-
e-![]() =
= ![]()
 =
= ![]()
![]() =
= ![]() T
T
![]() =
= ![]()
![]()
![]() 5
5
![]() 5 =
5 = ![]() fD(i) = 1 -
fD(i) = 1 - ![]() fD(i)
fD(i)![]() =
= ![]() T = 4 x 1 = 4
T = 4 x 1 = 4
![]() 5 = 1 -
5 = 1 - ![]() 1 +
1 + ![]() +
+ ![]() +
+ ![]() +
+ ![]()
![]() e-4 = 0, 37
e-4 = 0, 37