Sous-sections
Après avoir déterminé les caractéristiques électriques principales
d'une paire de conducteurs, on peut modéliser le fonctionnement électrique
d'une ligne en imaginant le système comme une succession de bouts
de lignes infinitésimaux; la figure 9.5 montre
un bout de ligne infinitésimal.
Figure 9.5:
Segment de ligne infinitésimal.
|
|
R
, L
, C
et G
sont appelés paramètres primaires
de la ligne avec
- R
= résistance linéique élémentaire, représentant la résistance
de la ligne par unité de longueur
[
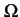 /m]
. Elle dépend en particulier
de la section et de la nature du conducteur,
/m]
. Elle dépend en particulier
de la section et de la nature du conducteur,
- L
= inductance linéique [H/m]
, modélisant la présence d'un flux
variable autour et entre les structures conductrices,
- C
= capacité linéique [F/m]
, caractérisant la capacité du diélectrique
constituant la ligne,
- G
= admittance linéique
[
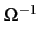 /m]
, représentant les pertes
diélectriques et les défauts d'isolation de la ligne. Elle dépend
de la nature des isolants.
/m]
, représentant les pertes
diélectriques et les défauts d'isolation de la ligne. Elle dépend
de la nature des isolants.
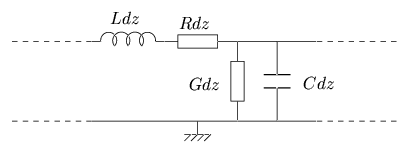
En mettant bout à bout des segments de ligne infinitésimaux et sur
base du schéma de la figure 9.6, on obtient
aisément le système d'équations suivantes, dites équations
des télégraphistes,
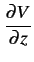 |
= |
RI + L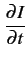 |
(9.7) |
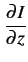 |
= |
GV + C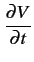 |
(9.8) |
Figure 9.6:
Modèle d'une ligne de transmission électrique.
|
|
La solution du système s'obtient en dérivant l'équation 9.7
par rapport à z
et en tenant compte de 9.8.
On obtient une équation aux dérivées partielles du second ordre
 = RGV + (RC + LG) = RGV + (RC + LG)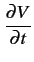 + LC + LC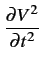 |
(9.9) |
Dans le cas d'une ligne sans perte (R = G = 0
),
 = LC = LC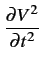 |
(9.10) |
ce qui correspond à une équation d'ondes bien connue dont la solution
est une combinaison linéaire de signaux sinusoïdaux
V(z, t) = (A cos kz + B sin kz)(C cos 2 ft + D sin 2 ft + D sin 2 ft) ft) |
(9.11) |
où A
, B
, C
et D
sont des constantes dont les
valeurs dépendent des conditions initiales.
En régime permanent,
V(z, t) = V(z)ej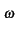 t
. La solution est
de la forme
t
. La solution est
de la forme
 = (R + jL = (R + jL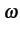 )(G + jC )(G + jC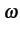 )V(z) = )V(z) = 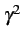 V(z) V(z) |
(9.12) |
En prenant une constante de propagation
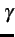 =
= 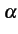 + j
+ j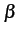 , on
obtient
, on
obtient
V(z) = Vie-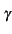 z + Vre z + Vre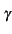 z z |
(9.13) |
L'onde est donc constituée d'une onde incidente (
Vie-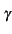 z
)
et d'une onde réfléchie (
Vre
z
)
et d'une onde réfléchie (
Vre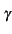 z
). De plus, on constate
que les deux ondes subissent une atténuation
e-
z
). De plus, on constate
que les deux ondes subissent une atténuation
e-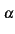 z
liée
au facteur
z
liée
au facteur 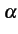 . On voit tout de suite que l'atténuation croît
avec la longueur de la ligne.
. On voit tout de suite que l'atténuation croît
avec la longueur de la ligne.
La présence d'une atténuation ne signifie pas que toute transmission
soit impossible mais bien que le signal est atténué dès qu'il y a
des pertes dans le conducteur, impliquant une longueur maximale de
la ligne. L'analyse en détail de la question montre que l'atténuation
dépend de la fréquence. En fait, elle augmente avec la fréquence.
Il est dès lors plus intéressant d'utiliser les basses fréquences
pour la transmission. Néanmoins, rien n'empêche d'utiliser les zones
d'atténuation plus importantes. C'est le mode de fonctionnement des
modems à haut débit ADSL dont le spectre d'utilisation est montré
à la figure 9.7.
Figure 9.7:
Spectre d'un signal ADSL.
|
|
Les paramètres primaires ne modélisent la ligne que d'une manière
microscopique. On leur préfère souvent les paramètres dits secondaires
suivants pour déterminer les propriétés macroscopiques du support:
Le facteur d'atténuation 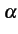 représente les pertes subies par
le signal électrique lors de la propagation le long de la ligne. Il
se mesure en injectant un signal à l'une des extrémités de la ligne
et en mesurant le signal reçu à l'autre extrémité.
représente les pertes subies par
le signal électrique lors de la propagation le long de la ligne. Il
se mesure en injectant un signal à l'une des extrémités de la ligne
et en mesurant le signal reçu à l'autre extrémité. 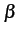 est lié
à la longueur d'onde
est lié
à la longueur d'onde 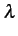 et à la vitesse de propagation v
de l'onde électromagnétique dans le support par
et à la vitesse de propagation v
de l'onde électromagnétique dans le support par
Les paramètres primaires et secondaires sont liés par les relations
suivantes
Ces équations sont générales et valables sur tout type de ligne. Toutefois,
certaines simplifications sont possibles en considérant un caractère
plutôt inductif ou pas de ligne, une fréquence d'utilisation élevée
ou non. D'autre part, on peut raisonnablement admettre que l'admittance
linéique est négligeable, autrement dit G = 0
, en présence d'un isolant
entre les conducteurs. Et donc,
Notes
- ...9.1
- Le Néper est lié au décibel par la relation suivante:
1 [Np] = 8, 68 [dB]
.
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27
![]() /m]
/m]
![]() /m]
/m]
![]() = RGV + (RC + LG)
= RGV + (RC + LG)![]() + LC
+ LC![]()
![]() = LC
= LC![]()
![]() ft + D sin 2
ft + D sin 2![]() ft)
ft)![]() t
t
![]() = (R + jL
= (R + jL![]() )(G + jC
)(G + jC![]() )V(z) =
)V(z) = ![]() V(z)
V(z)![]() =
= ![]() + j
+ j![]()
![]() z + Vre
z + Vre![]() z
z![]() z
z
![]() z
z
![]() z
z
![]()
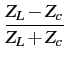
![]()
![]() =
= ![]() + j
+ j![]()
![]()
![]()
![]()
![]()
![]()
![]() =
= ![]() =
= ![]() =
= ![]()
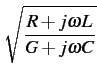
![]()
![]()
![]()
![]()
![]()
![]()