Sous-sections
La diaphonie est bien présente dans le réseau téléphonique. En effet,
les lignes sortent du central téléphonique dans des câbles pouvant
atteindre plusieurs centaines, voire milliers de paires. Cette proximité
entraîne des effets diaphoniques importants entre les paires.
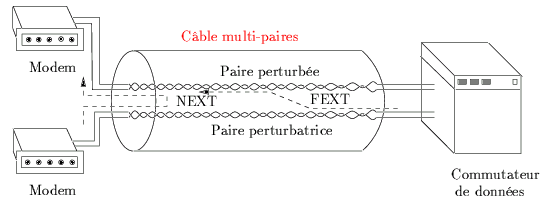
La figure 9.16 montre la situation
du réseau téléphonique. Le NEXT (Near-End Crosstalk)
et le FEXT (Far-End Crosstalk) représentent respectivement
la para et la télédiaphonie.
Figure 9.16:
Diaphonie dans le réseau téléphonique.
|
|
En raison de la structure du réseau, les caractéristiques locales
ne sont pas invariantes dans tout le réseau. L'approche analytique
consiste à simplifier la situation pour aboutir à des conclusions
de principe. On cherchera donc à établir une fonction de transfert
de puissance entre lignes de référence.
On distingue deux types de modèle pour expliquer les phénomènes de
diaphonie:
- le modèle des capacités non équilibrées et
- le modèle des inductances non équilibrées.
Nous allons étudier ces deux modèles.
Ce modèle considère deux paires voisines, placées au dessus d'un écran.
Comme le montre la figure 9.17, les quatre
fils sont caractérisés par une impédance propre, une admittance avec
les autres conducteurs et une capacité à une masse commune. On supposera
raisonnablement que la conductance entre fils est nulle parce que
les conducteurs sont enrobés d'un isolant.
Figure 9.17:
Modèle capacitif de deux paires.
|
|
Pour un système constitué de N + 1
conducteurs, on peut définir N
tensions et N
courants; ces valeurs correspondent à N
circuits.
L'utilisation usuelle d'un câble à N
conducteurs revient à considérer
N/2
paires, elles-mêmes organisées en quarte.
Ces paires servent à transmettre un signal en mode différentiel, c'est-à-dire
de type
Vi - Vi+1
. Pour arriver à N
circuits au total, il
reste un solde théorique de N/2
circuits. Mais ces derniers sont
délaissés en pratique en raison des effets diaphoniques inacceptables
qu'ils induisent.
Pour la facilité, on écrit les capacitances comme des admittances:
Y = j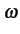 C
(on admet que G = 0
). Pour les calculs, nous utiliserons
des tensions référencées par rapport à la masse.
C
(on admet que G = 0
). Pour les calculs, nous utiliserons
des tensions référencées par rapport à la masse.
L'application de la loi des mailles donne les équations suivantes
V1(x +  x) x) |
= |
V1(x) - I1(x)Z1 x x |
(9.30) |
V2(x +  x) x) |
= |
V2(x) - I2(x)Z2 x x |
(9.31) |
V3(x +  x) x) |
= |
V3(x) - I3(x)Z3 x x |
(9.32) |
V4(x +  x) x) |
= |
V4(x) - I4(x)Z4 x x |
(9.33) |
et l'application de la loi des n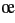 uds fournit les équations suivantes
uds fournit les équations suivantes
I1(x +  x) x) |
= |
I1(x) - V1(x +  x)Y1G x)Y1G x - [V1(x + x - [V1(x +  x) - V2(x + x) - V2(x +  x)]Y12 x)]Y12 x x |
|
| |
|
- [V1(x +  x) - V3(x + x) - V3(x +  x)]Y13 x)]Y13 x - [V1(x + x - [V1(x +  x) - V4(x + x) - V4(x +  x)]Y14 x)]Y14 x x |
|
I2(x +  x) x) |
= |
I2(x) - V2(x +  x)Y2G x)Y2G x - [V2(x + x - [V2(x +  x) - V1(x + x) - V1(x +  x)]Y12 x)]Y12 x x |
|
| |
|
- [V2(x +  x) - V3(x + x) - V3(x +  x)]Y23 x)]Y23 x - [V2(x + x - [V2(x +  x) - V4(x + x) - V4(x +  x)]Y24 x)]Y24 x x |
|
I3(x +  x) x) |
= |
I3(x) - V3(x +  x)Y3G x)Y3G x - [V3(x + x - [V3(x +  x) - V1(x + x) - V1(x +  x)]Y13 x)]Y13 x x |
|
| |
|
- [V3(x +  x) - V2(x + x) - V2(x +  x)]Y23 x)]Y23 x - [V3(x + x - [V3(x +  x) - V4(x + x) - V4(x +  x)]Y34 x)]Y34 x x |
|
I4(x +  x) x) |
= |
I4(x) - V4(x +  x)Y4G x)Y4G x - [V4(x + x - [V4(x +  x) - V1(x + x) - V1(x +  x)]Y13 x)]Y13 x x |
|
| |
|
- [V4(x +  x) - V2(x + x) - V2(x +  x)]Y24 x)]Y24 x - [V4(x + x - [V4(x +  x) - V3(x + x) - V3(x +  x)]Y34 x)]Y34 x x |
|
Dans toutes ces équations, on peut passer à la limite
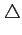 x
x 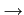 0
après avoir divisé tous les membres par
0
après avoir divisé tous les membres par
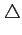 x
. Se rappelant
que la dérivée est définie par la formule suivante
x
. Se rappelant
que la dérivée est définie par la formule suivante
Les 8 équations s'expriment alors sous la forme matricielle
suivante
où
| A1 |
= |
- (Y1G + Y12 + Y13 + Y14) |
(9.36) |
| A2 |
= |
- (Y2G + Y12 + Y23 + Y24) |
(9.37) |
| A3 |
= |
- (Y3G + Y13 + Y23 + Y34) |
(9.38) |
| A4 |
= |
- (Y4G + Y14 + Y24 + Y34) |
(9.39) |
Les tensions utiles s'exprimant comme une différence de tensions,
on procède aux changements de variables suivants
| V1M |
= |
V1 - V2 |
(9.40) |
| V2M |
= |
V3 - V4 |
(9.41) |
| V1L |
= |
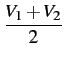 |
(9.42) |
| V2L |
= |
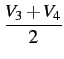 |
(9.43) |
| I1M |
= |
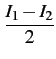 |
(9.44) |
| I2M |
= |
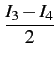 |
(9.45) |
| I1L |
= |
I1 + I2 |
(9.46) |
| I2L |
= |
I3 + I4 |
(9.47) |
Ces équations peuvent également être regroupées sous forme matricielle
![$\displaystyle \overrightarrow{S}=\underline{T}\left[\begin{array}{c} V_{1M} ...
... I_{1L} I_{2M} I_{2L}\end{array}\right]=\underline{T}\overrightarrow{S}'$](img1078.gif) |
(9.48) |
où T
est une matrice permettant d'effectuer le changement de variables
Dès lors,
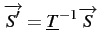 |
(9.50) |
L'ensemble s'écrit finalement
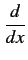 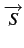 |
= |
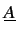 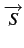 |
(9.51) |
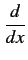 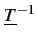 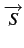 |
= |
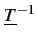 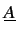 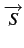 |
(9.52) |
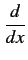 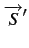 |
= |
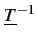 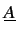 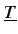 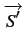 |
(9.53) |
La conséquence du changement de variables est le découplage des équations,
c'est-à-dire qu'il est possible d'exprimer les courants uniquement
en fonction des tensions. Dès lors, en remplaçant Y
par j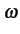 C
,
on obtient
C
,
on obtient
où
| a11 |
= |
C1G + C2G +4C12 + C13 + C14 + C23 + C24 |
(9.55) |
| a21 |
= |
a12 = 2C1G -2C2G +2C13 +2C14 -2C23 -2C24 |
(9.56) |
| a31 |
= |
a13 = - C13 + C14 + C23 - C24 |
(9.57) |
| a41 |
= |
a14 = - 2C13 -2C14 +2C23 +2C34 |
(9.58) |
| a22 |
= |
4C1G +4C2G +4C13 +4C14 +4C23 +4C24 |
(9.59) |
| a23 |
= |
a32 = - 2C13 +2C14 -2C23 +2C24 |
(9.60) |
| a24 |
= |
a42 = - 4C13 -4C14 -4C23 -4C24 |
(9.61) |
| a33 |
= |
C3G + C4G + C13 + C14 + C23 + C24 +4C34 |
(9.62) |
| a34 |
= |
a43 = 2C3G -2C4G +2C13 -2C14 +2C23 -2C24 |
(9.63) |
| a44 |
= |
4C3G +4C4G +4C13 +4C14 +4C23 +4C24 |
(9.64) |
Le paramètre a31
de ces équations détermine le couplage entre
la tension sur une paire et le courant induit dans l'autre paire.
Ce terme serait nul si toutes les capacitances étaient égales par
couple. C'est ce déséquilibre de capacités qui est à l'origine d'un
effet diaphonique; il s'exprime par 9.4
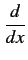 I2M = - I2M = - 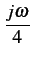 CM1M2V1M CM1M2V1M |
(9.65) |
où
CM1M2
est égal à a31
(ou a13
).
Cette équation détermine donc le courant l'évolution du courant perturbateur
dans la paire perturbatrice dû à une tension dans la paire perturbatrice.
Les termes a12
et a21
sont eux liés au mode commun.
Le modèles des inductances non équilibrées est similaire au précédent.
Les circuits sont représentés par une série d'effets inductifs tels
que repris à la figure 9.18.
Figure 9.18:
Modèle inductif de deux paires.
|
|
L'analyse détaillée de la question montre que la diaphonie se traduit
également par l'apparition d'un courant induit dans une paire dû à
une différence de tension appliquée à l'autre paire. Plus précisément,
où M
vaut
M1 + M2 + M3 + M4
.
Il apparaît donc que les effets des deux modèles fournissent un courant
perturbateur tel que
que l'on écrira plus généralement
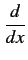 I2M = j I2M = j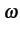 QM1M2V1M QM1M2V1M |
(9.68) |
où
QM1M2
tient compte des effets capacitifs
et inductifs.
Notes
- ...9.4
- L'équation 9.65 néglige le terme de diaphonie
dû à la tension V1L
de mode commun car, lors de l'installation
des lignes, l'opérateur s'arrange pour avoir un rapport de mode différentiel
à mode commun de 35
à 55 [dB]
.
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27
![]() C
C
![]() x)
x)![]() x
x![]() x)
x)![]() x
x![]() x)
x)![]() x
x![]() x)
x)![]() x
x![]() uds fournit les équations suivantes
uds fournit les équations suivantes
![]() x)
x)![]() x)Y1G
x)Y1G![]() x - [V1(x +
x - [V1(x + ![]() x) - V2(x +
x) - V2(x + ![]() x)]Y12
x)]Y12![]() x
x![]() x) - V3(x +
x) - V3(x + ![]() x)]Y13
x)]Y13![]() x - [V1(x +
x - [V1(x + ![]() x) - V4(x +
x) - V4(x + ![]() x)]Y14
x)]Y14![]() x
x![]() x)
x)![]() x)Y2G
x)Y2G![]() x - [V2(x +
x - [V2(x + ![]() x) - V1(x +
x) - V1(x + ![]() x)]Y12
x)]Y12![]() x
x![]() x) - V3(x +
x) - V3(x + ![]() x)]Y23
x)]Y23![]() x - [V2(x +
x - [V2(x + ![]() x) - V4(x +
x) - V4(x + ![]() x)]Y24
x)]Y24![]() x
x![]() x)
x)![]() x)Y3G
x)Y3G![]() x - [V3(x +
x - [V3(x + ![]() x) - V1(x +
x) - V1(x + ![]() x)]Y13
x)]Y13![]() x
x![]() x) - V2(x +
x) - V2(x + ![]() x)]Y23
x)]Y23![]() x - [V3(x +
x - [V3(x + ![]() x) - V4(x +
x) - V4(x + ![]() x)]Y34
x)]Y34![]() x
x![]() x)
x)![]() x)Y4G
x)Y4G![]() x - [V4(x +
x - [V4(x + ![]() x) - V1(x +
x) - V1(x + ![]() x)]Y13
x)]Y13![]() x
x![]() x) - V2(x +
x) - V2(x + ![]() x)]Y24
x)]Y24![]() x - [V4(x +
x - [V4(x + ![]() x) - V3(x +
x) - V3(x + ![]() x)]Y34
x)]Y34![]() x
x![]() x
x ![]() 0
0
![]() x
x
![]() f (x) =
f (x) = ![]()
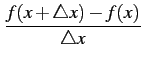
![]()
![]()
![]()
![]() =
= ![]()
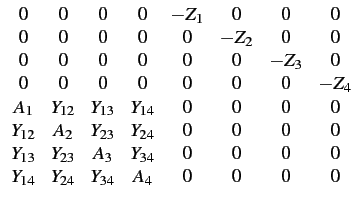
![]()
![]()
![]()
![]() =
= ![]()
![]()
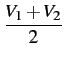
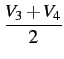
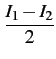
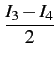
![$\displaystyle \overrightarrow{S}=\underline{T}\left[\begin{array}{c} V_{1M} ...
... I_{1L} I_{2M} I_{2L}\end{array}\right]=\underline{T}\overrightarrow{S}'$](img1078.gif)
![]() =
= ![]()
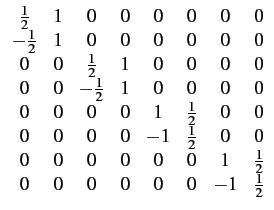
![]()
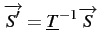
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() C
C
![]()
![]()
![]()
![]() = -
= - ![]()
![]()

![]()
![]()
![]()
![]() I2M
I2M ![]()
![]() V1M
V1M![]() I2M =
I2M = ![]()
![]() -
- ![]() CM1M2
CM1M2![]() V1M
V1M