symboles par seconde, la capacité par seconde est donnée par
Considérons le schéma de la figure 9.23.
Figure 9.23:
Calcul de la capacité de canal d'un canal binaire symétrique.
|
|
La capacité du canal s'exprime par
| Cs |
= |
max{p(xj)}I(X;Y) |
(9.103) |
| |
= |
max{p(xj)} H(X) - H(X| Y) H(X) - H(X| Y)![$\displaystyle \left.\vphantom{H(X)-H(X\vert Y)}\right]$](img1147.gif) |
(9.104) |
| |
= |
max{p(xj)} H(Y) - H(Y| X) H(Y) - H(Y| X)![$\displaystyle \left.\vphantom{H(Y)-H(Y\vert X)}\right]$](img1149.gif) |
(9.105) |
Calculons l'entropie conditionnelle H(Y| X)
. Pour ce faire, appliquons
la formule 9.96 adaptée. Pour la paire
entrée-sortie
(x0, y0)
, on obtient
H(Y| X)(x0, y0) = - p(x)0p(y0| x0) log2 p(y0| x0) p(y0| x0)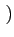 |
(9.106) |
Sachant que la probabilité d'émission du symbole x0
vaut 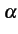 et que la probabilité conditionnelle
p(y0| x0)
vaut p
(cf. figure 9.23), on obtient
et que la probabilité conditionnelle
p(y0| x0)
vaut p
(cf. figure 9.23), on obtient
H(Y| X)(x0, y0) = - 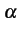 p log2p p log2p |
(9.107) |
En effectuant de même pour toutes les combinaisons entrée-sortie (
(x1, y0),(x0, y1)
et
(x1, y1)
) et en sommant les différentes contributions,
on trouve
| H(Y| X) |
= |
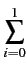  H(Y| X)(xi, yj) H(Y| X)(xi, yj) |
(9.108) |
| |
= |
- p log2p - q log2q |
(9.109) |
On constate donc que H(Y| X)
ne dépend que des caractéristiques
du canal, on parle d'entropie de canal. Dès lors,
| I(X;Y) = H(Y) + p log2p + q log2q |
(9.110) |
Pour maximiser cette quantité, on ne peut plus jouer que sur H(Y)
.
Le maximum que l'on peut obtenir avec un canal binaire est une valeur
unitaire pour H(Y)
. La capacité maximale de canal est alors
| Cs = 1 + p log2p + q log2q |
(9.111) |
Sur le schéma de la figure 9.23, q
représente la probabilité de prendre une décision erronée; c'est la
probabilité d'erreur. Dans le cas d'une modulation à deux états, la
probabilité d'erreur est liée au rapport signal à bruit par la relation
L'évolution de la capacité de canal en fonction du rapport signal
sur bruit est représentée à la figure 9.24.
On constate que, lorsque le rapport signal sur bruit tend vers l'infini
(c'est-à-dire que la probabilité d'erreur tend vers 0), la capacité
maximale du canal tend vers 1 bit.
Prenons le cas d'une modulation à quatre états (4-AM par exemple).
La matrice de canal se complique car il faut calculer plusieurs probabilités
d'erreur pour un symbole d'entrée donné.
Cependant, l'expression de la capacité de canal reste de la forme
où la valeur maximale de H(Y)
est de deux, la conséquence d'une
modulation à quatre états étant que l'on a deux bits par symbole et
où Hc
est un terme associé aux transitions de canal. Il est
alors intuitivement acceptable que la capacité de canal tende vers
deux quand le rapport signal à bruit tend vers l'infini. Le raisonnement
peut être répété pour des modulations à 16 voire 64 états. Les résultats
sont résumés à la figure 9.24.
Figure 9.24:
Capacité de canal pour différents types de modulation.
|
|
Dans le cas où l'on considère des alphabets d'entrée et de sortie
continus, le calcul de la capacité de canal s'en trouve très fortement
compliqué. Pour un canal blanc additif gaussien de moyenne nulle et
de variance
 , la sortie vaut
, la sortie vaut
Y = X + N(0, ) ) |
(9.114) |
Pour le calcul de la capacité de canal, on impose en outre une limitation
de la puissance d'entrée à
 .
.
Théorème 42
[SHANNON] Des calculs montrent
que la capacité d'un canal blanc additif gaussien de moyenne
nulle et de variance
 s'exprime par
où
s'exprime par
où
 représente le rapport
signal sur bruit.
représente le rapport
signal sur bruit.
Cette formule porte le nom de second théorème
de SHANNON. On constate que, dans le cas d'un
bruit important (


 ), le canal ne
parvient pas à transmettre de l'information. La figure 9.25
compare la limite théorique de SHANNON avec les capacités maximales
atteintes par les différentes techniques de modulation. Il est intéressant
de noter que la limite théorique de SHANNON correspond au cas
d'une modulation comportant un nombre infini d'états.
), le canal ne
parvient pas à transmettre de l'information. La figure 9.25
compare la limite théorique de SHANNON avec les capacités maximales
atteintes par les différentes techniques de modulation. Il est intéressant
de noter que la limite théorique de SHANNON correspond au cas
d'une modulation comportant un nombre infini d'états.
Figure 9.25:
Second théorème de SHANNON.
|
|
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27
![]() p(y0| x0)
p(y0| x0)![]()
![]()
![]() p log2p
p log2p![]()
![]() H(Y| X)(xi, yj)
H(Y| X)(xi, yj)![]() erfc
erfc![]()
![]()
![]()
![]()
![]() )
)![]()
![]()
![]() log2
log2![]() 1 +
1 + ![]()
![]()
![]()
![]()
![]()
![]()


