Le modèle développé ci-après aboutit à définir des signaux passe-bande
complexes et une fréquence de référence pour permettre la mise en
correspondance entre un signal passe-bande original et le signal passe-bas
de synthèse.
Dans un souci de rigueur, il conviendrait plutôt de parler de famille
de passe-bas équivalents. À l'évidence, toute fonction
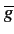 (t) = (g(t) + jz(t))e-2
(t) = (g(t) + jz(t))e-2 jf0t-j
jf0t-j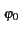 respecte l'égalité 2.3.
respecte l'égalité 2.3.
La détermination d'un type de passe-bas équivalent revient donc à
choisir une fonction particulière pour z(t)
. Comme on pourra s'en
apercevoir le choix n'est pas unique. Pour compliquer l'affaire, certains
auteurs [23] définissent le passe-bas équivalent en introduisant
un facteur de normalisation 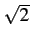 dans l'expression 2.3
afin d'éviter l'apparition d'un facteur 2 lors de l'analyse de systèmes
linéaires; on trouve les deux définitions dans la littérature.
dans l'expression 2.3
afin d'éviter l'apparition d'un facteur 2 lors de l'analyse de systèmes
linéaires; on trouve les deux définitions dans la littérature.
Notes
- ... signal2.2
-
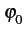 est souvent choisi nul par commodité. Cela ne nuit
en rien à la généralité des propos.
est souvent choisi nul par commodité. Cela ne nuit
en rien à la généralité des propos.
Sous-sections
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27
![]()
![]()