de la forme
s(t) = Re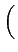 (m1(t) + jm2(t))e2 (m1(t) + jm2(t))e2 jfct+j jfct+j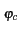 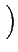 |
(2.4) |
Par comparaison avec la définition d'un passe-bas équivalent (relation 2.3),
le choix suivant s'impose
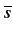 (t) = m1(t) + jm2(t) (t) = m1(t) + jm2(t) |
(2.5) |
La fréquence porteuse joue alors le rôle de fréquence de référence2.3. Ce passe-bas équivalent n'a pas de réelle signification physique
puisqu'il est de nature complexe. C'est néanmoins un signal de synthèse
fort commode, comme nous le verrons, pour traiter les signaux passant
dans un système linéaire.
Les signaux m1(t)
et m2(t)
sont appelés respectivement
composante en phase et composante
en quadrature de s(t)
, car
s(t) = m1(t)cos(2 fct + fct + 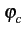 ) - m2(t)sin(2 ) - m2(t)sin(2 fct + fct + 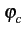 ) ) |
(2.6) |
Dans le cas d'une modulation numérique linéaire, les signaux m1(t)
et m2(t)
représentent une séquence d'impulsions mises en forme.
On peut aisément trouver les équivalents passe-bas des principales
modulations numériques.
Un signal numérique à 2n
états modulé en amplitude (2n
-ASK)
est de la forme
s(t) =  AkRect[0, T](t - kT)cos(2 AkRect[0, T](t - kT)cos(2 fct) fct) |
(2.7) |
où Ak
est une variable aléatoire pouvant prendre 2n
valeurs
différentes. Le passe-bas équivalent est tout simplement
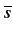 (t) = (t) =  AkRect[0, T](t - kT) AkRect[0, T](t - kT) |
(2.8) |
De même, sachant qu'un signal numérique à 2n
états modulé en
phase (2n
-PSK) est de la forme
s(t) =  Rect[0, T](t - kT)cos(2 Rect[0, T](t - kT)cos(2 fct + fct + 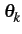 ) ) |
(2.9) |
où
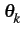 est une variable aléatoire pouvant prendre 2n
valeurs différentes dans l'intervalle [0, 2
est une variable aléatoire pouvant prendre 2n
valeurs différentes dans l'intervalle [0, 2 ]
. Le passe-bas équivalent
est
]
. Le passe-bas équivalent
est
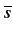 (t) = (t) =  Rect[0, T](t - kT)ej Rect[0, T](t - kT)ej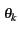 |
(2.10) |
En effet, en prenant
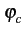 = 0
,
= 0
,
s(t) = Re![$\displaystyle \left(\vphantom{\sum_{k=-\infty}^{+\infty}Rect_{[0,T]}(t-kT)e^{j\theta_{k}}e^{2\pi jf_{c}t}}\right.$](img239.gif)  Rect[0, T](t - kT)ej Rect[0, T](t - kT)ej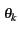 e2 e2 jfct jfct![$\displaystyle \left.\vphantom{\sum_{k=-\infty}^{+\infty}Rect_{[0,T]}(t-kT)e^{j\theta_{k}}e^{2\pi jf_{c}t}}\right)$](img240.gif) = =  Rect[0, T](t - kT)cos(2 Rect[0, T](t - kT)cos(2 fct + fct + 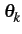 ) ) |
(2.11) |
Notes
- ... référence2.3
- Ce choix convient dans bon nombre de cas mais il arrive qu'un autre
choix soit plus judicieux; c'est la facilité de formulation résultante
qui guidera le choix final.
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27
![]() fct +
fct + ![]() ) - m2(t)sin(2
) - m2(t)sin(2![]() fct +
fct + ![]() )
)![]() AkRect[0, T](t - kT)cos(2
AkRect[0, T](t - kT)cos(2![]() fct)
fct)![]() (t) =
(t) = ![]() AkRect[0, T](t - kT)
AkRect[0, T](t - kT)![]() Rect[0, T](t - kT)cos(2
Rect[0, T](t - kT)cos(2![]() fct +
fct + ![]() )
)![]()
![]() ]
]
![]() (t) =
(t) = ![]() Rect[0, T](t - kT)ej
Rect[0, T](t - kT)ej![]()
![]() = 0
= 0
![]()
![]() Rect[0, T](t - kT)ej
Rect[0, T](t - kT)ej![]() e2
e2![]() jfct
jfct![]() =
= ![]() Rect[0, T](t - kT)cos(2
Rect[0, T](t - kT)cos(2![]() fct +
fct + ![]() )
)