Sous-sections
Jusqu'à présent, nous avons étudié les signaux modulés. Néanmoins,
le principe de ramener le signal en bande de base s'applique à tous
les signaux de type passe-bande. Cela nécessite pourtant quelques
précautions si l'on veut éviter des recouvrements de spectre à l'origine.
Prenons un signal g(t)
réel et déterministe. Le principe
de base consiste à effacer une partie du spectre avant de procéder
à un déplacement fréquentiel. L'opération est sans perte d'information
si l'on se rappelle que le spectre d'un signal réel est tel que
Re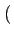  (- f ) (- f ) |
= |
Re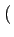 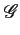 (f ) (f )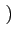 |
(2.12) |
Im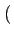 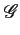 (- f ) (- f ) |
= |
- Im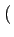 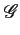 (f ) (f )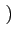 |
(2.13) |
L'exploitation de la symétrie permet de ne considérer que les fréquences
positives durant les calculs, à condition bien sûr de reconstituer
les fréquences négatives pour rétablir la nature du signal réel en
fin de calculs.
Soit donc le filtre
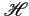 (f )
supprimant les fréquences négatives;
par la même occasion, il amplifie les fréquences positives d'un facteur
2
de manière à conserver le même niveau d'énergie. Ce filtre se
caractérise par la transmittance
(f )
supprimant les fréquences négatives;
par la même occasion, il amplifie les fréquences positives d'un facteur
2
de manière à conserver le même niveau d'énergie. Ce filtre se
caractérise par la transmittance
qui peut également se mettre sous la forme
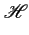
(
f )= 1 +
sgn(
f )
Étant donné que la transformée de FOURIER de la fonction sgn
est donnée par
sgn(
t)


on peut utiliser la propriété de dualité de la transformée de FOURIER
pour déduire que

 sgn
sgn(
f )
On arrive alors à l'expression de la réponse impulsionnelle du filtre
h(
t) =
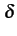
(
t) +

On définit ensuite la transformée de HILBERT d'un signal.
Définition 13
[Transformée de HILBERT]
Soit un signal g(t)
. Sa transformée de HILBERT, notée
#MATH604#(T)
MATHEND000#, vaut
Par cette définition,
ga(t) = g(t) + j (t) (t) |
(2.18) |
Le signal analytique est donc composé d'une partie réelle, qui n'est
autre que le signal original, et d'une partie imaginaire qui en est
la transformée de HILBERT. L'apparition d'une composante imaginaire
ne doit pas nous étonner car elle résulte de la rupture de symétrie
dans le spectre. La norme du signal analytique est appelée enveloppe
du signal.
Le signal
 (t)
porte aussi le nom de signal en
quadrature du signal d'entrée. Cette appellation provient des caractéristiques
du filtre
(t)
porte aussi le nom de signal en
quadrature du signal d'entrée. Cette appellation provient des caractéristiques
du filtre
 . En effet, la transmittance de ce filtre
vaut - jsgn(f )
. Dès lors,
. En effet, la transmittance de ce filtre
vaut - jsgn(f )
. Dès lors,
 (f )= - jsgn(f ) (f )= - jsgn(f )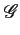 (f ) (f ) |
(2.19) |
Autrement dit, les fréquences positives et négatives subissent toutes
un déphasage de
- 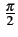 . Par la même occasion, on remarque
que la transformée de HILBERT occupe la même bande de fréquence
que le signal original.
. Par la même occasion, on remarque
que la transformée de HILBERT occupe la même bande de fréquence
que le signal original.
Propriété 14
L'énergie (ou la puissance) d'un signal et celle de sa transformée
de HILBERT sont égales.
Démonstration
L'énergie de la transformée de HILBERT d'un signal
vaut
Or
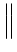  (f ) (f )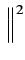 |
= |
 - jsgn(f ) - jsgn(f )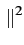 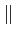 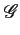 (f ) (f ) |
(2.21) |
| |
= |
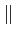 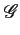 (f ) (f ) |
(2.22) |
Propriété 15
[35, page 96] Un signal est orthogonal à sa transformée
de HILBERT. Pour un signal d'énergie,
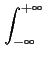 g(t) g(t) (t)dt = 0 (t)dt = 0 |
(2.23) |
et pour un signal de puissance
Calculons tout d'abord la transformée de HILBERT d'un cosinus.
Soit
g(t) = cos(2 fct)
. Le spectre de signal vaut
fct)
. Le spectre de signal vaut
 (f )= (f )=  |
(2.25) |
d'où, par application de la relation 2.19,
qui n'est autre que le transformée de FOURIER d'un sinus. Ainsi,
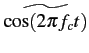 = sin(2 = sin(2 fct) fct) |
(2.28) |
Ce résultat ne doit pas nous étonner car il découle d'un déphasage
du cosinus par ajout d'une phase
-  . Le même raisonnement
conduit aisément au résultat suivant.
. Le même raisonnement
conduit aisément au résultat suivant.
Propriété 16
[Transformée de HILBERT
d'un signal modulé] Soit un signal g(t)
en bande de base,
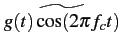 = g(t)sin(2 = g(t)sin(2 fct) fct) |
(2.29) |
Le signal analytique peut être utilisé pour construire un signal passe-bas
équivalent. En effet, il suffit de ramener le signal analytique près
de l'origine par une translation de son spectre. Un moyen commode
consiste à prendre la fréquence de référence f0
du signal passe-bande
pour effectuer le déplacement. Mais ce choix n'est nullement obligatoire.
Définition 17
[Enveloppe complexe du signal]
Le signal obtenu par décalage du signal analytique le long de l'axe
fréquentiel porte le nom d'enveloppe complexe du signal original.
Elle sera notée eg(t)
.
Par définition, l'enveloppe complexe et son spectre sont respectivement
liés à leur équivalent analytique par les relations
eg(t) = ga(t)e-2 jf0t jf0t |
(2.30) |
 g(f )= g(f )=  a(f + f0) a(f + f0) |
(2.31) |
La démarche adoptée a permis de construire l'enveloppe complexe à
partir du signal de départ. Pour se convaincre de l'utilité de l'enveloppe
complexe comme passe-bas équivalent, déterminons le lien inverse.
Un calcul simple montre que
| g(t) |
= |
Re ga(t) ga(t) |
(2.32) |
| |
= |
Re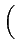 eg(t)e2 eg(t)e2 jf0t jf0t |
(2.33) |
Il s'agit donc bien d'une forme valide de passe-bas équivalent tel
que définie par la relation 2.3.
Il nous reste maintenant à déterminer des moyens pratiques pour calculer
l'enveloppe complexe d'un signal. Pour ce faire, on décompose l'enveloppe
complexe en sa partie réelle et sa partie imaginaire
| eg(t) = gI(t) + jgQ(t) |
(2.34) |
Nous avons pris le soin de faire référence au signal g
pour des
raisons qui apparaîtront bientôt. gI(t)
s'obtient comme suit
| gI(t) |
= |
Re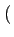 eg(t) eg(t) |
(2.35) |
| |
= |
Re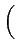 ga(t)e-2 ga(t)e-2 jf0t jf0t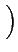 |
(2.36) |
| |
= |
g(t)cos(2 f0t) + f0t) +  (t)sin(2 (t)sin(2 f0t) f0t) |
(2.37) |
De même,
| gQ(t) |
= |
Im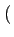 eg(t) eg(t) |
(2.38) |
| |
= |
Im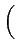 ga(t)e-2 ga(t)e-2 jf0t jf0t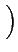 |
(2.39) |
| |
= |
- g(t)sin(2 f0t) + f0t) +  (t)cos(2 (t)cos(2 f0t) f0t) |
(2.40) |
Les signaux gI(t)
et gQ(t)
sont appelés composantes
de RICE ou composantes en quadrature. Sur le
plan théorique, on peut les calculer très simplement à partir du schéma
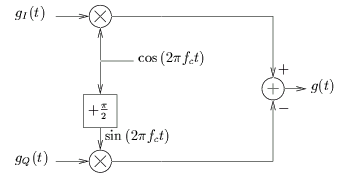
décrit à la figure 2.3.
Figure 2.3:
Schéma de calcul de la composante en phase de RICE.
|
|
L'intérêt des composantes de RICE est clair lorsqu'on détermine
le signal de départ à partir de l'enveloppe complexe. En effet,
| g(t) |
= |
Re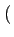 ga(t) ga(t) |
(2.41) |
| |
= |
Re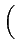 eg(t)e2 eg(t)e2 jf0t jf0t |
(2.42) |
| |
= |
Re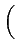 (gI(t) + jgQ(t))e2 (gI(t) + jgQ(t))e2 jf0t jf0t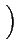 |
(2.43) |
| |
= |
gI(t)cos(2 f0t) - gQ(t)sin(2 f0t) - gQ(t)sin(2 f0t) f0t) |
(2.44) |
Cette dernière expression traduit un résultat important: tout signal
passe-bande peut s'exprimer comme la somme de deux signaux confinés
à l'intérieur de l'intervalle de fréquences
[- 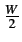 ,
,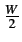 ]
et modulés en quadrature.
]
et modulés en quadrature.
La figure 2.4 montre comment reconstituer
le signal original à partir de ses composantes de RICE.
Figure 2.4:
Schéma de reconstitution d'un signal à partir de ses composantes de
RICE.
|
|
L'enveloppe complexe peut aussi s'écrire sous la forme d'une amplitude
instantanée et d'une phase instantanée
eg(t) = ag(t)ej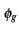 (t) (t) |
(2.45) |
On a alors les trois relations
| ag(t) |
= |
 |
(2.46) |
 (t) (t) |
= |
tan-1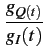 |
(2.47) |
| g(t) |
= |
ag(t)cos(2 f0t + f0t +  (t)) (t)) |
(2.48) |
Dès lors, on trouve un second résultat important: tout signal passe-bande
peut s'exprimer sous la forme d'un signal modulé en phase et en amplitude.
Le passage de g(t)
dans un détecteur de crête produit ag(t)
.
D'autre part, moyennant la suppression de la modulation résiduelle,
un détecteur de phase ou un discriminateur de fréquences sera en mesure
de déterminer l'allure de la modulation angulaire.
Les expressions 2.37 et 2.40
de calcul des composantes de RICE, pour rigoureuses qu'elles
soient, ne sont guère pratiques car elles exigent la détermination
préalable de la transformée de HILBERT. Un moyen très facile
consiste à procéder à l'instar d'un démodulateur d'amplitude: on multiplie
le signal original par
2 cos(2 f0t)
(ou
2 sin(2
f0t)
(ou
2 sin(2 f0t)
)
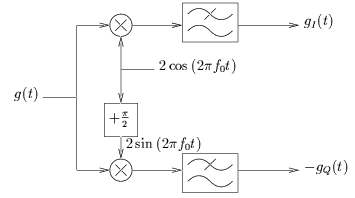
et on applique un filtre passe-bas, comme illustré par le schéma 2.5.
f0t)
)
et on applique un filtre passe-bas, comme illustré par le schéma 2.5.
En effet,
g(t) x 2 cos(2 f0t) f0t) |
= |
2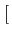 gI(t)cos(2 gI(t)cos(2 f0t) - gQ(t)sin(2 f0t) - gQ(t)sin(2 f0t) f0t)![$\displaystyle \left.\vphantom{g_{I}(t)\cos(2\pi f_{0}t)-g_{Q}(t)\sin(2\pi f_{0}t)}\right]$](img290.gif) cos(2 cos(2 f0t) f0t) |
(2.49) |
| |
= |
2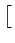 gI(t)cos2(2 gI(t)cos2(2 f0t) - gQ(t)sin(2 f0t) - gQ(t)sin(2 f0t)cos(2 f0t)cos(2 f0t) f0t)![$\displaystyle \left.\vphantom{g_{I}(t)\cos^{2}(2\pi f_{0}t)-g_{Q}(t)\sin(2\pi f_{0}t)\cos(2\pi f_{0}t)}\right]$](img292.gif) |
(2.50) |
| |
= |
gI(t) + gI(t)cos(4 f0t) - gQ(t)sin(4 f0t) - gQ(t)sin(4 f0t) f0t) |
(2.51) |
Un filtrage passe-bas fournit donc bien gI(t)
.
Figure 2.5:
Schéma de calcul pratique des composantes de RICE.
|
|
Les composantes de RICE occupent une bande de fréquences qui
n'est pas fondamentalement plus large que celle de l'enveloppe complexe.
Pour le montrer, calculons le spectre de gI(t)
. Comme
gI(t) = 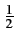
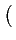 eg(t) + eg * (t)
eg(t) + eg * (t) ,
,
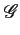 I(f )= I(f )=   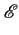 g(f )+ g(f )+ 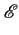 g * (- f ) g * (- f ) |
(2.52) |
Dès lors, si la transformée
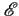 g(f )
est
nulle
g(f )
est
nulle
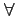 f :
f : 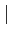 f
f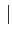 > fsup
, le spectre de la composante
en phase est confiné dans l'intervalle de fréquences
[- fsup, + fsup]
.
> fsup
, le spectre de la composante
en phase est confiné dans l'intervalle de fréquences
[- fsup, + fsup]
.
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27
![]() (f )
(f )
![]() (f )=
(f )= ![]()

![]() (f )= 1 + sgn(f )
(f )= 1 + sgn(f )
![]()
![]()
![]()
![]() sgn(f )
sgn(f )
![]() (t) +
(t) + ![]()
![]()
![]()
![]() (t) +
(t) + ![]()
![]()
![]()
![]()
![]() (t) = g(t)
(t) = g(t) ![]()
![]()
![]() (t)
(t)![]() (t)
(t)
![]()
![]()
![]()
![]()
![]() (t)
(t)![]() dt =
dt = ![]()
![]()
![]() (f )
(f )![]() df
df![]()
![]() (f )
(f )![]()
![]() - jsgn(f )
- jsgn(f )![]()
![]()
![]() (f )
(f )![]()
![]()
![]() (f )
(f )![]()
![]() g(t)
g(t)![]() (t)dt = 0
(t)dt = 0![]()
![]()
![]() g(t)
g(t)![]() (t)dt = 0
(t)dt = 0![]() fct)
fct)
![]() (f )=
(f )= 
![]() (f )
(f )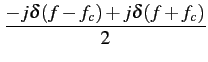

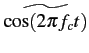 = sin(2
= sin(2![]() fct)
fct)![]()
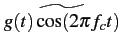 = g(t)sin(2
= g(t)sin(2![]() fct)
fct)![]() jf0t
jf0t![]() g(f )=
g(f )= ![]() a(f + f0)
a(f + f0)![]() ga(t)
ga(t)![]()
![]() eg(t)e2
eg(t)e2![]() jf0t
jf0t![]()
![]() ga(t)
ga(t)![]()
![]() eg(t)e2
eg(t)e2![]() jf0t
jf0t![]()
![]() (gI(t) + jgQ(t))e2
(gI(t) + jgQ(t))e2![]() jf0t
jf0t![]()
![]() f0t) - gQ(t)sin(2
f0t) - gQ(t)sin(2![]() f0t)
f0t)![]() ,
,![]() ]
]
![]() (t)
(t)
![]() (t)
(t)![]()
![]() f0t +
f0t + ![]() (t))
(t))![]() f0t)
f0t)
![]() f0t)
f0t)
![]() f0t)
f0t)![]() gI(t)cos(2
gI(t)cos(2![]() f0t) - gQ(t)sin(2
f0t) - gQ(t)sin(2![]() f0t)
f0t)![]() cos(2
cos(2![]() f0t)
f0t)![]() gI(t)cos2(2
gI(t)cos2(2![]() f0t) - gQ(t)sin(2
f0t) - gQ(t)sin(2![]() f0t)cos(2
f0t)cos(2![]() f0t)
f0t)![]()
![]() f0t) - gQ(t)sin(4
f0t) - gQ(t)sin(4![]() f0t)
f0t)![]()
![]() eg(t) + eg * (t)
eg(t) + eg * (t)![]()
![]() I(f )=
I(f )= ![]()
![]()
![]() g(f )+
g(f )+ ![]() g * (- f )
g * (- f )![]()
![]() g(f )
g(f )
![]() f :
f : ![]() f
f![]() > fsup
> fsup