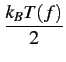 |
(3.16) |
La relation 3.15 est commode à bien des égards; en effet, la densité spectrale est uniforme et exprimée comme le produit de constantes par la température absolue. Cette relation a donc été généralisée pour traiter le bruit en général.
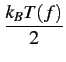 |
(3.16) |
On peut comprendre l'idée de l'introduction de la température de bruit
ponctuelle en revenant un instant à la nature stochastique des phénomènes.
En effet, considérons deux signaux stochastiques de bruit N(t)
Si l'on a affaire à un dipôle dont la densité spectrale est concentrée
autour d'une position fréquentielle centrale, on peut définir la bande
passante de bruit W
![]() (f )+
(f )+ ![]() (f )
(f )
![]() kBT
kBT
![]() kBT'
kBT'
![]() kB(T + T') =
kB(T + T') = ![]() kBT''
kBT''
3.3.2.2 Température de bruit
Pbd(f )= kBTW
(3.17)
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27