Soit
m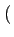 t
t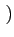 un signal en bande de base préalablement mis
en forme; il s'agit par exemple d'un signal NRZ. Un modulateur
numérique transforme le signal modulant m(t)
en fournissant le
signal modulé s(t)
suivant
un signal en bande de base préalablement mis
en forme; il s'agit par exemple d'un signal NRZ. Un modulateur
numérique transforme le signal modulant m(t)
en fournissant le
signal modulé s(t)
suivant
s(t) = Re![$\displaystyle \left(\vphantom{\psi\left[m(t)\right] e^{j\left(2\pi f_{c}t+\varphi_{c}\right)}}\right.$](img489.gif) 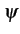 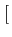 m(t) m(t)![$\displaystyle \left.\vphantom{m(t)}\right]$](img492.gif) ej ej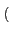 2 2 fct + fct + 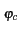  ![$\displaystyle \left.\vphantom{\psi\left[m(t)\right] e^{j\left(2\pi f_{c}t+\varphi_{c}\right)}}\right)$](img495.gif) |
(4.1) |
où fc
est la fréquence porteuse du signal modulé et
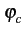 une phase constante.
une phase constante.
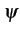
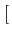 m(t)
m(t)![$ \left.\vphantom{m(t)}\right]$](img498.gif) est une fonction du
signal m(t)
et constitue l'enveloppe complexe es(t)
du signal modulé. Étant donnée la forme de l'équation (4.1),
le signal s(t)
est réel et passe-bande autour de la fréquence fc
.
est une fonction du
signal m(t)
et constitue l'enveloppe complexe es(t)
du signal modulé. Étant donnée la forme de l'équation (4.1),
le signal s(t)
est réel et passe-bande autour de la fréquence fc
.
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27
![]() t
t![]()
![]()
![]()
![]() m(t)
m(t)![]()