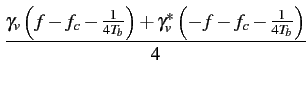Dans le cas des modulations linéaires à décalage, l'expression (4.65)
de l'enveloppe complexe ne permet pas un calcul direct de sa densité
spectrale de puissance, en raison de la présence du facteur
ejk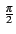 .
Afin de résoudre ce problème, nous allons introduire une nouvelle
fréquence porteuse fc'
et une nouvelle enveloppe complexe v(t)
pour laquelle le calcul de la densité spectrale de puissance sera
possible :
.
Afin de résoudre ce problème, nous allons introduire une nouvelle
fréquence porteuse fc'
et une nouvelle enveloppe complexe v(t)
pour laquelle le calcul de la densité spectrale de puissance sera
possible :
| s(t) |
= |
Re es(t) ej es(t) ej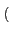 2 2 fct + fct + 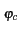 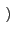 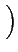 |
(4.73) |
| |
= |
Re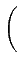 es(t) e-j2 es(t) e-j2 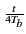 ej ej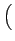 2 2 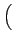 fc + fc + 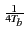 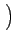 t + t + 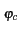 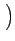 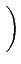 |
(4.74) |
| |
= |
Re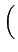 v(t) ej v(t) ej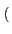 2 2 fc't + fc't + 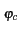 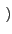 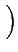 |
(4.75) |
où nous avons posé
| v(t) |
= |
e-j2 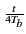 es(t) es(t) |
(4.76) |
| fc' |
= |
fc + 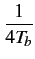 |
(4.77) |
Si nous connaissons la densité spectrale de puissance du signal complexe
v(t)
, il est possible de calculer la densité spectrale de puissance
du signal modulé par le biais de la formule
que nous avons démontrée précédemment. Nous allons à présent montrer
que v(t)
peut se mettre sous la forme (4.24)
pour laquelle nous sommes à même de calculer la densité spectrale
de puissance. En fait,
| v(t) |
= |
 Ak g(t - kTb) ejk Ak g(t - kTb) ejk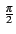 e-j2 e-j2 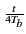 |
(4.79) |
| |
= |
 Ak g(t - kTb) e-j Ak g(t - kTb) e-j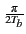 (t-kTb) (t-kTb) |
(4.80) |
| |
= |
 Ak h(t - kTb) Ak h(t - kTb) |
(4.81) |
où nous avons posé
h(t) = g(t) e-j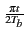 |
(4.82) |
Le signal h(t)
correspond à un nouveau signal de mise en forme
dont la transformée de FOURIER se déduit du signal g(t)
La densité spectrale de puissance du signal v(t)
s'obtient alors
en adaptant la formule (4.27)
Nous avons à présent à notre disposition tous les outils nécessaires
au calcul de la densité spectrale de puissance de signaux numériques
linéaires à décalage.
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27
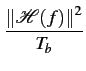
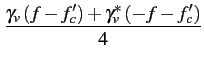 =
=