La façon la plus simple de satisfaire l'équation 5.19
consiste à choisir pour
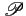 (f )
une impulsion de forme rectangulaire
(f )
une impulsion de forme rectangulaire
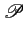 (f ) (f ) |
= |
 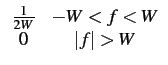 |
(5.20) |
| |
= |
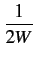 rect[-W,+W] rect[-W,+W]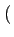 f f |
(5.21) |
où la bande de base du système W
est définie par
W = 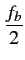 = =  |
(5.22) |
La condition est donc bien satisfaite. Cette équation permet de dire
qu'aucune fréquence nécessaire ne dépasse la moitié du débit binaire.
On en déduit qu'une fonction p(t)
qui satisferait le critère de
NYQUIST est, comme il avait été signalé précédemment, le sinus
cardinal:
p(t) = 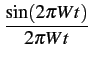 = sinc(2Wt) = sinc(2Wt) |
(5.23) |
Une telle fonction p(t)
(ou
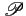 (f )
) caractérise le canal
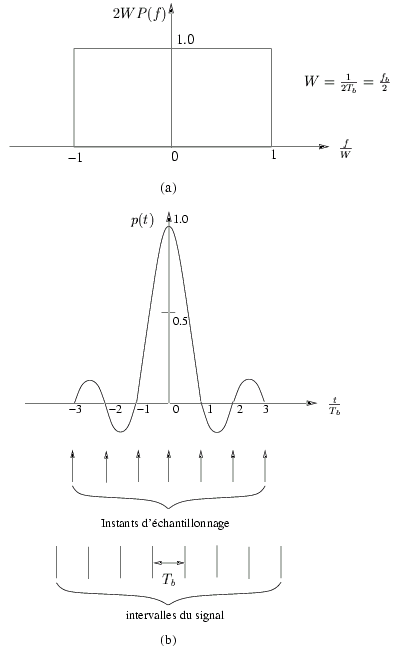
idéal de NYQUIST. Les figures 5.2.(a) et .5.2.(b)
montre les fonctions p(t)
et
(f )
) caractérise le canal
idéal de NYQUIST. Les figures 5.2.(a) et .5.2.(b)
montre les fonctions p(t)
et
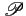 (f )
. p(t)
peut dès
lors être vue comme la réponse impulsionnelle d'un filtre passe bas
idéal de fréquence de coupure correspondant à W
.
(f )
. p(t)
peut dès
lors être vue comme la réponse impulsionnelle d'un filtre passe bas
idéal de fréquence de coupure correspondant à W
.
Figure 5.2:
Canal idéal de Nyquist.
|
|
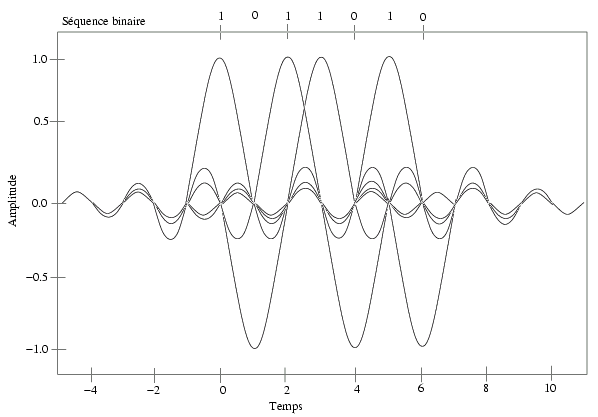
À la figure 5.2.(b), on voit également les différents
instants d'échantillonage. Il est clair que, si le signal reçu y(t)
est échantillonné aux instants
t = 0,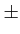 Tb,
Tb,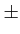 2Tb, ...
, les
impulsions
2Tb, ...
, les
impulsions
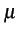 p(t - iTb)
(
i = 0,
p(t - iTb)
(
i = 0,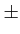 1,
1,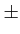 2, ...
) n'interfèrent
pas entre elles. Cette condition est illustrée à la figure 5.3
pour la séquence binaire 1011010. On constate dès lors qu'aux instants
d'échantillonnage, tous les sinus cardinal relatif aux symboles perturbateurs
sont nuls.
2, ...
) n'interfèrent
pas entre elles. Cette condition est illustrée à la figure 5.3
pour la séquence binaire 1011010. On constate dès lors qu'aux instants
d'échantillonnage, tous les sinus cardinal relatif aux symboles perturbateurs
sont nuls.
Figure 5.3:
Une série d'impulsions correspondant à la séquence 1011010.
|
|
Il existe cependant des raisons pour lesquelles l'impulsion en sinus
cardinal ne peut être utilisée en pratique:
- elle nécessite que
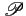 (f )
soit constante sur l'intervalle
de fréquence [- W, + W]
et nulle partout ailleurs. Cela est pratiquement
irréalisable en raison des transitions abruptes en
(f )
soit constante sur l'intervalle
de fréquence [- W, + W]
et nulle partout ailleurs. Cela est pratiquement
irréalisable en raison des transitions abruptes en 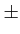 W
(un filtre
passe-bas idéal n'est pas réalisable),
W
(un filtre
passe-bas idéal n'est pas réalisable),
- la fonction p(t)
décroît en 1/| t|
pour | t|
élevé; elle décroît
donc très lentement, les sinus cardinal se répercuteront donc sur
des échantillons lointains. Il y a dès lors très peu de marge d'erreur
acceptable sur les instants d'échantillonnage car si on n'échantillonne
pas tout à fait au bon moment, tous les sinus cardinaux sont non nuls,
ce qui donne une erreur cumulée importante.
Pour évaluer cet effet d'erreur d'échantillonnage, considérons que
l'on échantillonne le signal y(t)
en
t = ti + 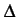 t
, où
t
, où 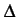 t
est le décalage temporel. Pour la clarté, on suppose que ti = 0
.
En l'absence de bruit, nous avons donc
t
est le décalage temporel. Pour la clarté, on suppose que ti = 0
.
En l'absence de bruit, nous avons donc
y(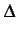 t) t) |
= |
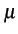  Ak p( Ak p(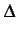 t - kTb) t - kTb) |
(5.24) |
| |
= |
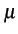  Ak Ak ![$\displaystyle {\frac{{\sin[2\pi W(\Delta t-kT_{b})]}}{{2\pi W(\Delta t-kT_{b})}}}$](img839.gif) |
(5.25) |
Sachant que
sin[2 W( W(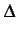 t - kTb)] t - kTb)] |
= |
sin(2 W W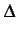 t)cos(2 t)cos(2 WkTb) WkTb) |
(5.26) |
| |
|
-cos(2 W W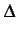 t)sin(2 t)sin(2 WkTb) WkTb) |
(5.27) |
| |
= |
(- 1)ksin(2 W W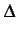 t) t) |
(5.28) |
Comme 2WTb = 1
par définition, nous pouvons réécrire
y(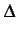 t) = t) = 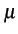 A0 sinc(2W A0 sinc(2W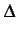 t) + t) +  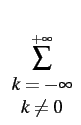 Ak Ak |
(5.29) |
Le premier terme correspond au symbole désiré, tandis que la série
représente l'interférence inter-symboles dues à l'erreur 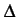 t
.
Il est malheureusement possible que cette série diverge, provoquant
des décisions erronées au récepteur.
t
.
Il est malheureusement possible que cette série diverge, provoquant
des décisions erronées au récepteur.
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27
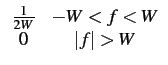
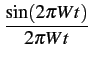 = sinc(2Wt)
= sinc(2Wt)![]() Tb,
Tb,![]() 2Tb, ...
2Tb, ...
![]() p(t - iTb)
p(t - iTb)
![]() 1,
1,![]() 2, ...
2, ...
![]() (f )
(f )
![]() W
W
![]() t
t
![]() t
t
![]() t)
t)![]()
![]() Ak p(
Ak p(![]() t - kTb)
t - kTb)![]()
![]() Ak
Ak ![$\displaystyle {\frac{{\sin[2\pi W(\Delta t-kT_{b})]}}{{2\pi W(\Delta t-kT_{b})}}}$](img839.gif)
![]() W(
W(![]() t - kTb)]
t - kTb)]![]() W
W![]() t)cos(2
t)cos(2![]() WkTb)
WkTb)![]() W
W![]() t)sin(2
t)sin(2![]() WkTb)
WkTb)![]() W
W![]() t)
t)![]() t) =
t) = ![]() A0 sinc(2W
A0 sinc(2W![]() t) +
t) + 
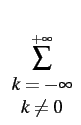 Ak
Ak
![]() t
t