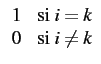Le but poursuivi est, comme mentionné précédemment, de choisir la
forme de p(t)
de manière à minimiser, voire éliminer, le terme
d'interférence. Or, nous avons vu que p(t)
est liée à gE(t)
,
h(t)
et gR(t)
. Cependant, en général, la fonction de transfert
du canal de transmission h(t)
est fixée et il est donc impossible
de la modifier pour minimiser l'interférence inter-symboles. Il reste
cependant deux degrés de liberté: l'impulsion de mise en forme gE(t)
et la réponse impulsionnelle du filtre de réception gR(t)
. Le
terme d'interférence étant exprimé en fonction de l'impulsion p(t)
,
nous allons simplement déterminer une forme pour p(t)
telle que
l'interférence s'annulle complètement. Les fonctions gE(t)
et
gR(t)
pourront ensuite être obtenues en exploitant l'équation 5.8.
Le décodeur extrait la séquence de coefficients Ak
en échantillonnant
la sortie du filtre y(t)
toutes les Tb
secondes. Pour le
i
-ème bit, le décodage à interférence inter-symboles nulle survient
si les contributions
Akp(iTb - kTb)
sont nulles pour k 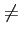 i
.
Dès lors, il faut que l'impulsion p(t)
vérifie la condition
i
.
Dès lors, il faut que l'impulsion p(t)
vérifie la condition
p(iTb - kTb) =  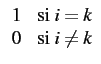 |
(5.12) |
où p(0) = 1
par normalisation. Si p(t)
vérifie cette condition,
il n'y pas d'interférence inter-symboles et la réception est parfaite
en l'absence de bruit. On constate déjà, intuitivement, qu'une
fonction sinus cardinal permettrait de remplir cette condition.
Du point de vue de la synthèse du système, il est intéressant de reprendre
la condition 5.12 dans le domaine fréquentiel.
Comme la propriété que doit vérifier p(t)
est donnée en des points
bien précis (au droit des échantillons), considérons la version échantillonnée
de p(t)
représentée par la séquence d'échantillons
{p(mTb)}
pour
m = 0,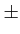 1,
1,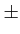 2, ...
Le signal
2, ...
Le signal
ps(t) = 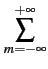 p(mTb) p(mTb)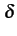 (t - mTb) (t - mTb) |
(5.13) |
représente alors une version échantillonnée du signal p(t)
. Par
le théorème d'échantillonnage, il est facile de calculer la transformée
de FOURIER du signal ps(t)
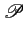 s(f )= fb s(f )= fb 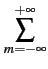 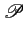 (f - mfb) (f - mfb) |
(5.14) |
où
fb = 1/Tb
est le débit binaire (ou rythme) exprimé
en [b/s]
. On remarque dès lors une répétition du spectre autour
de tous les multiples entiers de la fréquence d'échantillonnage. La
fonction
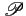 s(f )
peut encore s'écrire sous la forme
s(f )
peut encore s'écrire sous la forme
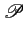 s(f )= s(f )= 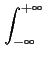 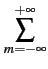  p(mTb) p(mTb)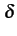 (t - mTb) (t - mTb)![$\displaystyle \left.\vphantom{p(mT_{b})\delta(t-mT_{b})}\right]$](img832.gif) e-2 e-2 jft dt jft dt |
(5.15) |
mais vu que la somme se réduit au terme correspondant à m = 0
, on
peut encore écrire
 s(f ) s(f ) |
= |
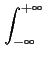 p(0) p(0) (t)e-2 (t)e-2 jtf dt jtf dt |
(5.16) |
| |
= |
1 |
(5.17) |
Il nous reste maintenant à combiner les équations et pour obtenir
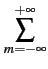 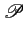 (f - mfb) = Tb (f - mfb) = Tb |
(5.18) |
Nous pouvons à présent énoncer le critère de NYQUIST pour une
transmission en bande de base idéale en l'absence de bruit.
Proposition 22
[Critère de NYQUIST]
La transformée de FOURIER
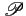 (f )
de l'impulsion
p(t)
élimine totalement l'interférence inter-symboles pour des
échantillons pris toutes les Tb
secondes si elle vérifie la
condition
(f )
de l'impulsion
p(t)
élimine totalement l'interférence inter-symboles pour des
échantillons pris toutes les Tb
secondes si elle vérifie la
condition
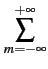 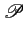 (f - mfb) = Tb (f - mfb) = Tb |
(5.19) |
Rappelons que la transformée
 (f )
dépend du système dans
son ensemble; cela inclut le filtre de mise en forme, la transmittance
du canal et le filtre de réception.
(f )
dépend du système dans
son ensemble; cela inclut le filtre de mise en forme, la transmittance
du canal et le filtre de réception.
Sous-sections
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27
![]() i
i
![]() 1,
1,![]() 2, ...
2, ...
![]() s(f )
s(f )
![]() (f )
(f )
![]() (f )
(f )