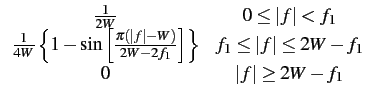Nous pouvons trouver une parade aux difficultés rencontrées avec le
canal idéal de NYQUIST en augmentant le bande passante d'une
valeur ajustable entre W
et 2W
. Nous allons spécifier la fonction
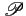 (f )
, en considérant trois termes de la condition 5.18,
et restreindre l'intervalle de fréquence étudié à [- W, + W]
. On obtient
donc une forme approchée du critère de NYQUIST:
(f )
, en considérant trois termes de la condition 5.18,
et restreindre l'intervalle de fréquence étudié à [- W, + W]
. On obtient
donc une forme approchée du critère de NYQUIST:
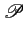 (f )+ (f )+ 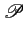 (f - 2W) + (f - 2W) + 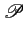 (f + 2W) = (f + 2W) = 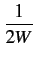 , - W , - W 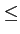 f f 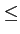 W W |
(5.30) |
Il est possible de déterminer un ensemble de fonctions
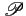 (f )
qui vérifient cette dernière condition. Une forme spéciale de la fonction
(f )
qui vérifient cette dernière condition. Une forme spéciale de la fonction
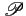 (f )
souvent utilisée en pratique est l'impulsion
en cosinus surélevé dont le spectre est donné par
(f )
souvent utilisée en pratique est l'impulsion
en cosinus surélevé dont le spectre est donné par
La constante f1
et la bande de base W
sont liées par
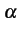 = 1 - = 1 - 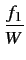 |
(5.32) |
où 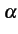 est un paramètre, appelé facteur de rolloff,
qui indique l'excès en bande passante nécessaire par rapport au canal
idéal de NYQUIST. La bande passante du système BT
est
maintenant égale à
est un paramètre, appelé facteur de rolloff,
qui indique l'excès en bande passante nécessaire par rapport au canal
idéal de NYQUIST. La bande passante du système BT
est
maintenant égale à
BT = 2W - f1 = W(1 + 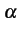 ) ) |
(5.33) |
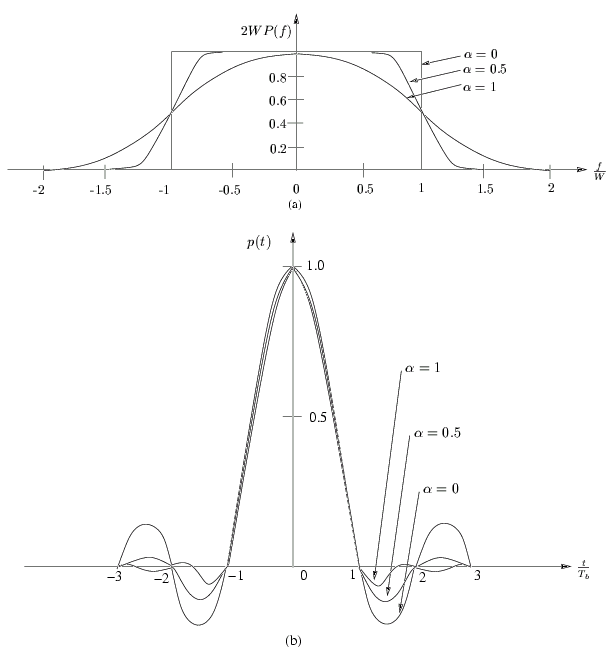
Les fonctions
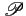 (f )
et p(t)
sont respectivement représentées
aux figures 5.4.(a) et 5.4.(b) pour
(f )
et p(t)
sont respectivement représentées
aux figures 5.4.(a) et 5.4.(b) pour
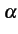 = 0
,
= 0
,
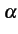 = 0, 5
et 1
. Pour
= 0, 5
et 1
. Pour 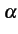 = 0
, l'impulsion
correspond au canal idéal de NYQUIST.
= 0
, l'impulsion
correspond au canal idéal de NYQUIST.
Figure 5.4:
Impulsion en cosinus surélevé.
|
|
L'impulsion p(t)
est simplement la transformée de FOURIER
inverse de
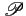 (f )
(f )
La fonction p(t)
est formée par le produit de deux facteurs: le
facteur sinc(2Wt)
qui correspond au canal idéal et une fonction
qui décroît en 1/| t|2
lorsque | t|
est grand. Le premier facteur
assure que la fonction p(t)
passe par zéro aux instants d'échantillonnage
ti = i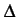 t
tandis que le second facteur réduit l'extension
temporelle de l'impulsion de telle sorte que l'erreur
t
tandis que le second facteur réduit l'extension
temporelle de l'impulsion de telle sorte que l'erreur 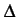 t
est considérablement réduite. Pour
t
est considérablement réduite. Pour 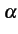 = 1
, l'extension temporelle
de l'impulsion est minimale. L'erreur
= 1
, l'extension temporelle
de l'impulsion est minimale. L'erreur 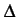 t
diminue donc lorsque
t
diminue donc lorsque
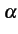 augmente. Cependant, la bande passante est d'autant plus
grande que
augmente. Cependant, la bande passante est d'autant plus
grande que 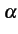 est grand, pour atteindre sa valeur maximale
2W
-soit le double de la bande passante nécessaire pour le canal
idéal de NYQUIST-, lorsque
est grand, pour atteindre sa valeur maximale
2W
-soit le double de la bande passante nécessaire pour le canal
idéal de NYQUIST-, lorsque 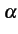 = 1
. Un compromis existe
donc entre la bande passante est la diminution de l'interférence inter-symboles.
Typiquement, une valeur de
= 1
. Un compromis existe
donc entre la bande passante est la diminution de l'interférence inter-symboles.
Typiquement, une valeur de
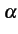 = 0.3
convient.
= 0.3
convient.
La synthèse d'un système de télécommunications numérique est rendue
difficile par le fait que c'est la fonction p(t)
qui doit posséder
une réponse impulsionnelle en forme de cosinus surélevé. Or, p(t)
résulte de la mise en cascade de trois systèmes (gE(t)
, h(t)
et gR(t)
). La synthèse de ces systèmes doit donc être telle
que l'ensemble doit être caractérisé par un cosinus surélevé.
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27
![]() (f )
(f )
![]()
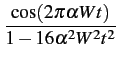
![]()
![]() t
t
![]() t
t
![]() = 1
= 1
![]() t
t
![]()
![]()
![]() = 1
= 1
![]() = 0.3
= 0.3