Les descripteurs statistiques décrits précédemment ne fournissent pas d'information concernant la nature périodique qu'une texture peut présenter. Ainsi, la texture de fond d'images (petits carrés obliques) de la figure 7.3 présente un caractère périodique qu'aucun descripteur introduit précédemment ne pourra mettre en lumière.
La matrice de co-occurrence introduite ci-après va nous offrir un premier moyen de caractériser la périodicité et la directivité des textures.
L'idée consiste à étudier la texture au moyen d'une fenêtre B d'observation
de la texture en comptabilisant le nombre de paires de pixels distants
de d qui présentent une différence ![]() z en niveaux de gris.
En plus de la distance, on tient compte de la direction définie par
toute paire de pixels.
z en niveaux de gris.
En plus de la distance, on tient compte de la direction définie par
toute paire de pixels.
Une matrice de co-occurrence est définie au moyen d'une relation géométrique
R entre deux pixels
(x1, y1) et
(x2, y2). Un exemple
de relation géométrique simple est
| x2 | = | x1 + 1 | (7.10) |
| y2 | = | y1 | (7.11) |
La matrice de co-occurrence CR(i, j) est carrée et de dimension L×L, où L est le nombre de niveaux de gris présents dans B. Les indices de la matrice de co-occurrence sont donc les niveaux de gris de la texture étudiée. La matrice CR(i, j) se construit comme suit :
| P90o, d(i, j) = |
(7.12) |
| P0o, d(i, j) = |
(7.13) |
Il est également possible de définir d'autres matrices correspondant aux directions 45o et 135o.
Exemple. Soit l'image suivante comportant L = 4 niveaux de gris (l = 0, 1, 2, 3) :
f (x, y) =  |
(7.14) |
P0o, 1 =   |
(7.15) |
L'analyse de textures sur base de la matrice de co-occurrence est fondée sur l'occurrence répétée d'une configuration typique dans la texture; cette configuration varie rapidement en fonction de la distance pour des textures fines et lentement pour des textures plus grossière. Les matrices de co-occurrence sont généralement utilisées par des algorithmes automatiques, à des fins d'identification par exemple. Seuls des cas simples, comme celui décrit ci-après, permettent une interprétation intuitive du contenu d'une matrice de co-occurrence.
Considérons la texture suivante comportant deux niveaux de gris 0 et 1:
|
(7.16) |
P0o, 1 = 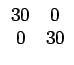 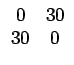 |
(7.17) |
P0o, 2 = 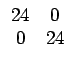 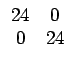 |
(7.18) |
Les matrices de co-occurrence permettent donc de caractériser la répétition de motifs dans une texture. Néanmoins, il faut remarquer que la taille d'une matrice de co-occurrence est proportionnelle au nombre de niveaux de gris de la texture. Pour L = 256, il faudrait donc des matrices carrées de taille 256×256. De plus, il faut considérer une matrice par couple (direction, d), ce qui entraîne un nombre assez élevé de descripteurs de texture.
À partir des matrices de co-occurrence, on a créé toute une série de nouveaux descripteurs (en nombre restreint cette fois-ci) permettant de mettre en évidence les paramètres les plus importants de ces matrices de co-occurrence.
C'est simplement la valeur maximale normalisée d'une des matrices ou de toutes les matrices de co-occurrence considérées.
Le moment d'ordre k d'une matrice de co-occurrence CR(i, j) est défini par
| (7.19) |
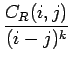 , i , i |
(7.20) |
| C(k, n) = |
(7.21) |
| H = - |
(7.22) |