11.3.3 Méthode du filtrage de la rétroprojection
L'idée de base qui se cache derrière la méthode dite du filtrage de
la rétroprojection est illustrée à la figure 11.12 pour la
reconstruction d'un point objet. Les principes de reconstruction sont
ici les suivants:
- Pour chaque angle
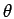 , on ``étend'' les valeurs de la projection
(qui, pour un point objet, ne sont non-nulles que dans une petite
région de s) sur la bande de direction
, on ``étend'' les valeurs de la projection
(qui, pour un point objet, ne sont non-nulles que dans une petite
région de s) sur la bande de direction
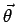 qui passe
par le point objet. On parle de rétroprojection des projections.
qui passe
par le point objet. On parle de rétroprojection des projections.
- On additionne le résultat de la rétroprojection de chaque projection
pour obtenir une image
fB(x, y) proche de f (x, y).
- On observe que
fB(x, y) est une version floue de f (x, y) avec
valeurs non-nulles en-dehors du support de f (x, y). On cherche alors
un filtre de déconvolution 2D qui permet de retrouver f (x, y) à
partir de
fB(x, y).
Figure 11.12:
Rétroprojection des projections pour un point objet.
|
|
La figure 11.13 montre le résultat
fB(x, y) correspondant
à l'image f (x, y) définie à la figure 11.8.
Figure 11.13:
Résultat de la rétroprojection pour un fantôme composé de 3 points
objet.
|
|
La représentation mathématique de l'image
fB(x, y) = fB(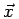 )
est
)
est
fB(x, y) = 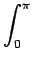 d d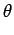 g( g(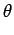 , s = , s = 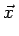 . .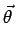 ) = ) = 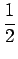 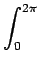 d d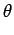 g( g(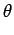 , s = , s = 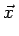 . .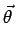 ). ). |
(11.8) |
Quelques calculs sont nécessaires pour trouver la relation entre
fB(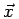 ) et
f (
) et
f (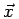 ). Tout d'abord, on remplace
g(
). Tout d'abord, on remplace
g(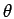 , s)
par l'inverse de sa transformée de FOURIER dans l'expression
de
fB(
, s)
par l'inverse de sa transformée de FOURIER dans l'expression
de
fB(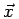 ) et on utilise le théorème du profil central pour
trouver
) et on utilise le théorème du profil central pour
trouver
fB(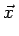 ) ) |
= |
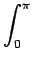 d d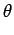 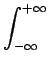 d d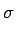 e2 e2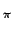 j j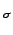 ( (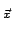 . .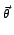 ) ( ) (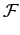 1g)( 1g)(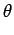 , ,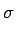 ) ) |
(11.9) |
| |
= |
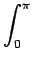 d d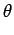 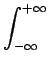 d d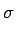 e2 e2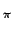 j j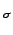 ( (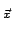 . .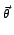 ) ( ) (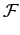 2f )( 2f )(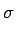 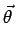 ) ) |
(11.10) |
Ensuite, on effectue le changement de variables
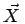 =
= 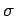
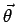 ,
avec jacobien
J = 1/|
,
avec jacobien
J = 1/|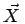 |, pour obtenir le résultat
|, pour obtenir le résultat
fB(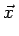 ) = ) = 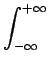 dX dX 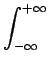 dY e2 dY e2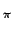 j j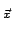 . .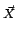 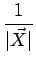 ( (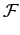 2f )( 2f )(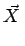 ). ). |
(11.11) |
Cette formule nous apprend que les transformées de FOURIER
de
fB(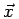 ) et
f (
) et
f (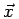 ) sont reliées par le filtre
1/|
) sont reliées par le filtre
1/|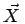 |.
On a donc la relation
|.
On a donc la relation
(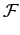 2fB)( 2fB)(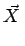 ) = ) = 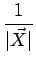 ( (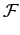 2f )( 2f )(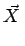 ) )  ( (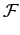 2f )( 2f )(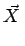 ) = | ) = |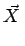 | ( | (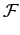 2fB)( 2fB)(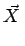 ). ). |
(11.12) |
De là, on décrit l'algorithme du filtrage de la rétroprojection comme
suit:
- Rétroprojection des projections pour obtenir
fB(
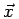 ).
).
- Calcul de la transformée de FOURIER de
fB(
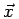 ),
application du filtre |
),
application du filtre |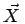 | et calcul de la transformée de
FOURIER inverse du résultat.
| et calcul de la transformée de
FOURIER inverse du résultat.
L'étape de déconvolution est très difficile à implémenter en pratique
parce que la transformée de FOURIER de
fB(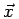 )
n'existe pas au sens classique (elle n'existe qu'au sens des distributions),
et aussi parce que
fB(
)
n'existe pas au sens classique (elle n'existe qu'au sens des distributions),
et aussi parce que
fB(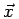 ) n'est pas à support compact (même
si
f (
) n'est pas à support compact (même
si
f (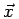 ) l'est), alors que le calcul de sa transformée de
FOURIER ne peut se faire numériquement qu'à partir d'une
grille de taille finie. En pratique, pour obtenir des images de qualité
satisfaisante en utilisant la méthode du filtrage de la rétroprojection,
il faut calculer l'image
fB(
) l'est), alors que le calcul de sa transformée de
FOURIER ne peut se faire numériquement qu'à partir d'une
grille de taille finie. En pratique, pour obtenir des images de qualité
satisfaisante en utilisant la méthode du filtrage de la rétroprojection,
il faut calculer l'image
fB(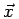 ) sur une grille de pixels
trois à quatre fois plus grande que celle utilisée pour
f (
) sur une grille de pixels
trois à quatre fois plus grande que celle utilisée pour
f (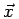 ).
On se retrouve alors avec un algorithme beaucoup plus lent que la
méthode dite de rétroprojection des projections filtrées, avec un
nombre d'opérations qui peut aller jusqu'à
O(16N
).
On se retrouve alors avec un algorithme beaucoup plus lent que la
méthode dite de rétroprojection des projections filtrées, avec un
nombre d'opérations qui peut aller jusqu'à
O(16N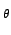 Q2) + O(8Q2log 2Q)
pour reconstruire
f (
Q2) + O(8Q2log 2Q)
pour reconstruire
f (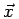 ) sur une grille de Q×Q pixels.
) sur une grille de Q×Q pixels.
Marc Van Droogenbroeck. Tous droits réservés.
2003-09-30
![]() )
est
)
est