Table des matières of 2.3.1 Périodicité intrinsèque

2.3.1 Périodicité intrinsèque

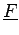
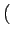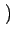La périodicité est une propriété importante de la transformée de FOURIER discrète. La transformée est définie par une matrice d'éléments $\underline{{F}}$ $\left(\vphantom{u,v}\right.$ u, v $\left.\vphantom{u,v}\right)$ pour u = 0, ..., M - 1 et v = 0, ..., N - 1. Si on permet aux indices u et v de prendre d'autres valeurs, on obtient une transformée périodique et une image périodique:

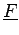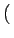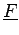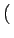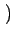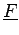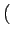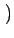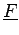$\displaystyle \underline{{F}}$ $\displaystyle \left(\vphantom{u,-v}\right.$ u, - v $\displaystyle \left.\vphantom{u,-v}\right)$ = $\displaystyle \underline{{F}}$ $\displaystyle \left(\vphantom{u,N-v}\right.$ u, N - v $\displaystyle \left.\vphantom{u,N-v}\right)$ $\displaystyle \underline{{F}}$ $\displaystyle \left(\vphantom{-u,v}\right.$ - u, v $\displaystyle \left.\vphantom{-u,v}\right)$ = $\displaystyle \underline{{F}}$ $\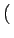displaystyle \left(\vphantom{M-u,v}\right.$ M - u, v $\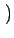displaystyle \left.\vphantom{M-u,v}\right)$

(2.16)

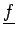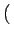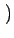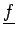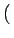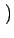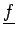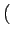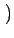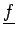$\displaystyle \underline{{f}}$ $\displaystyle \left(\vphantom{-m,n}\right.$ - m, n $\displaystyle \left.\vphantom{-m,n}\right)$ = $\displaystyle \underline{{f}}$ $\displaystyle \left(\vphantom{M-m,n}\right.$ M - m, n $\displaystyle \left.\vphantom{M-m,n}\right)$ $\displaystyle \underline{{f}}$ $\displaystyle \left(\vphantom{m,-n}\right.$ m, - n $\displaystyle \left.\vphantom{m,-n}\right)$ = $\displaystyle \underline{{f}}$ $\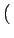displaystyle \left(\vphantom{m,N-n}\right.$ m, N - n $\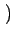displaystyle \left.\vphantom{m,N-n}\right)$

(2.17)

Plus généralement,

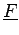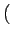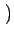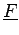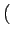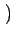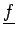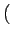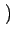$\displaystyle \underline{{F}}$ $\displaystyle \left(\vphantom{aM+u,\, bN+v}\right.$ aM + u, bN + v $\displaystyle \left.\vphantom{aM+u,\, bN+v}\right)$ = $\displaystyle \underline{{F}}$ $\displaystyle \left(\vphantom{u,v}\right.$ u, v $\displaystyle \left.\vphantom{u,v}\right)$ $\displaystyle \underline{{f}}$ $\displaystyle \left(\vphantom{aM+m,\, bN+n}\right.$ aM + m, bN + n $\displaystyle \left.\vphantom{aM+m,\, bN+n}\right)$ = $\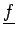displaystyle \underline{{f}}$ (m, n)

(2.18)

où a et b sont des entiers. Ces propriétés ne doivent pas nous étonner car elles résultent de l'échantillonnage dans les deux plans.

La figure 2.1 montre une image ainsi que le module de sa transformée de FOURIER calculée par le logiciel Matlab sur base de la formule 2.10.

Figure: L'image Lena et le module de sa transformée de FOURIER discrète.

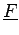
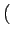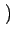Une remarque toute particulière est à faire au sujet de la visualisation de la transformée de FOURIER discrète. La composante fréquentielle $\underline{{F}}$ $\left(\vphantom{0,0}\right.$ 0, 0 $\left.\vphantom{0,0}\right)$ , appelée composante continue ou composante DC , se trouve en haut et à gauche de l'image alors qu'on a l'habitude de voir cette composante située au milieu de l'image. En utilisant les propriétés de périodicité, il est possible d'observer le module de la transformée de FOURIER d'une manière plus conventionnelle (cf. figure 2.2). Le spectre modifié par décalage de l'image Lena est donné à la figure 2.3.

**Figure 2.2:** Décalage du spectre pour arriver à centrer l'origine.

**Figure:** Visualisation du module du spectre de l'image Lena après centrage de l'origine.