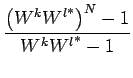 |
(2.19) |
En majorité, la DFT dispose des mêmes propriétés que son homologue continu (linéarité, translation spatiale, multiplication, convolution, ...), mis à part la nature périodique de l'image et de sa transformée suite aux échantillonnages effectués dans les deux domaines. On peut donc à souhait profiter des propriétés connues pour faciliter le calcul. En plus de ces propriétés, la nature discrète de la DFT permet de bénéficier d'autres avantages.
Les vecteurs Wk qui composent la matrice de FOURIER sont orthogonaux entre eux. La démonstration de cette propriété est simple. En effet, le produit scalaire de deux vecteurs (distincts) quelconques donne
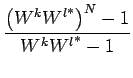 |
(2.19) |
| (2.20) |
Les vecteurs de base sont bien donc orthogonaux entre eux. De plus, ce sont les valeurs propres de la matrice de FOURIER (voir [37] pour la démonstration), ce qui signifie que l'application de la matrice de FOURIER diagonalise toute image périodique.
La transformée de FOURIER discrète peut être implémentée
de manière efficace malgré le fait que la matrice
![]() soit pleine. La raison pour laquelle il est possible de réduire le
nombre d'opérations intervenant dans le calcul matriciel tient au
fait que tous les vecteurs de base sont des multiples d'un même vecteur.
Cela permet de factoriser plus efficacement la matrice en série de
matrices creuses. Les algorithmes qui en découlent font partie de
la famille des transformées de FOURIER rapides (notée FFT).
soit pleine. La raison pour laquelle il est possible de réduire le
nombre d'opérations intervenant dans le calcul matriciel tient au
fait que tous les vecteurs de base sont des multiples d'un même vecteur.
Cela permet de factoriser plus efficacement la matrice en série de
matrices creuses. Les algorithmes qui en découlent font partie de
la famille des transformées de FOURIER rapides (notée FFT).
Détails pratiques. Remarquons que la formule 2.11
peut encore s'écrire sous la forme
| (2.21) |
Le calcul d'une FFT est le plus efficace lorsque N est une puissance de 2: N = 2k. Lorsque la taille de l'image n'est pas une puissance de 2, il est d'usage de compléter l'image en lui ajoutant des pixels de valeur nulle jusqu'à obtention de la taille adéquate. Cette démarche n'est pas sans entraîner certains inconvénients car elle modifie la résolution spectrale du résultat. On peut, pour éviter ce désagrément, recourir à des implémentations plus complexes de FFT qui particularisent le calcul pour des puissances autres que 2. Lorsqu'une telle implémentation n'est pas disponible, on pourra toujours recourir à l'application pure et simple de la définition, mais au détriment du temps de calcul!
Quelque soit l'implémentation choisie, le calcul d'une transformée de FOURIER manipule des nombres complexes et il fournit des valeurs complexes. La manipulation n'en est pas toujours commode. C'est pourquoi, certains chercheurs ont proposé des transformées qui reposent sur des simplifications de la transformée de FOURIER. La transformée de HADAMARD et la transformée en cosinus discrète font partie de ces familles de transformées à valeurs entières ou réelles.