Table des matières of 2.5 La transformée en cosinus discrète

Il existe 4 définitions de la transformée en cosinus discrète, parfois notées DCT-1, DCT-2, DCT-3, et DCT-4. Ces définitions diffèrent par les conditions limites qu'elles imposent aux bords^2.1.

La transformée la plus utilisée en traitement et compression d'images est la DCT-2 dont la définition suit. D'un point de vue théorique, cette variante présuppose que l'image a été miroirisée le long de ses bords car, dans ce cas, la transformée de FOURIER de la séquence miroirisée est rigoureusement égale à la DCT-2 de la séquence originale.

Nous faisons l'hypothèse que l'image est carrée de dimension N×N. Soit la matrice de transformation $\underline{{C}}_{{NN}}^{}$ $\left(\vphantom{k,l}\right.$ k, l $\left.\vphantom{k,l}\right)$ définie par

$\displaystyle \underline{{C}}_{{NN}}^{}$ $\displaystyle \left(\vphantom{k,l}\right.$ k, l $\displaystyle \left.\vphantom{k,l}\right)$ = $\displaystyle \left\{\vphantom{ \begin{array}{ccc} \frac{1}{\sqrt{N}} & & l=0\\... ...}\cos\left[\frac{\left(2k+1\right)l\pi}{2N}\right] & & sinon\end{array}}\right.$ $\displaystyle \begin{array}{ccc} \frac{1}{\sqrt{N}} & & l=0\\ \sqrt{\frac{2}{N}}\cos\left[\frac{\left(2k+1\right)l\pi}{2N}\right] & & sinon\end{array}$

(2.26)

Définition 6 La transformée en cosinus discrète DCT et son inverse sont données par

$\displaystyle \underline{{F}}$ = $\displaystyle \underline{{C}}_{{NN}}^{}$ $\displaystyle \underline{{f}}$ $\displaystyle \underline{{C}}_{{NN}}^{{T}}$ $\displaystyle \underline{{f}}$ = $\displaystyle \underline{{C}}_{{NN}}^{{T}}$ $\displaystyle \underline{{F}}$ $\displaystyle \underline{{C}}_{{NN}}^{}$

(2.27)

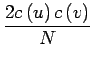$\displaystyle \underline{{F}}$ $\displaystyle \left(\vphantom{u,v}\right.$ u, v $\displaystyle \left.\vphantom{u,v}\right)$ = $\displaystyle {\frac{{2c\left(u\right)c\left(v\right)}}{{N}}}$ $\displaystyle \sum_{{m=0}}^{{N-1}}$ $\displaystyle \sum_{{n=0}}^{{N-1}}$ $\displaystyle \underline{{f}}$ $\displaystyle \left(\vphantom{m,n}\right.$ m, n $\displaystyle \left.\vphantom{m,n}\right)$ cos $\displaystyle \left(\vphantom{\frac{2m+1}{2N}u\pi}\right.$ $\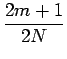displaystyle {\frac{{2m+1}}{{2N}}}$ u $\displaystyle \pi$ $\displaystyle \left.\vphantom{\frac{2m+1}{2N}u\pi}\right)$ cos $\displaystyle \left(\vphantom{\frac{2n+1}{2N}v\pi}\right.$ $\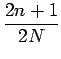displaystyle {\frac{{2n+1}}{{2N}}}$ v $\displaystyle \pi$ $\displaystyle \left.\vphantom{\frac{2n+1}{2N}v\pi}\right)$

(2.28)

u = 0, 1, ..., N - 1 v = 0, 1, ..., N - 1

(2.29)

c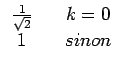 $\displaystyle \left(\vphantom{k}\right.$ k $\displaystyle \left.\vphantom{k}\right)$ = $\displaystyle \left\{\vphantom{ \begin{array}{ccc} \frac{1}{\sqrt{2}} & & k=0\\ 1 & & sinon\end{array}}\right.$ $\displaystyle \begin{array}{ccc} \frac{1}{\sqrt{2}} & & k=0\\ 1 & & sinon\end{array}$

(2.30)

$\displaystyle \underline{{f}}$ $\displaystyle \left(\vphantom{m,n}\right.$ m, n $\displaystyle \left.\vphantom{m,n}\right)$ = $\displaystyle {\frac{{2}}{{N}}}$ $\displaystyle \sum_{{m=0}}^{{N-1}}$ $\displaystyle \sum_{{n=0}}^{{N-1}}$ c $\displaystyle \left(\vphantom{u}\right.$ u $\displaystyle \left.\vphantom{u}\right)$ c $\displaystyle \left(\vphantom{v}\right.$ v $\displaystyle \left.\vphantom{v}\right)$ $\displaystyle \underline{{F}}$ $\displaystyle \left(\vphantom{u,v}\right.$ u, v $\displaystyle \left.\vphantom{u,v}\right)$ cos $\displaystyle \left(\vphantom{\frac{2m+1}{2N}u\pi}\right.$ $\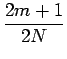displaystyle {\frac{{2m+1}}{{2N}}}$ u $\displaystyle \pi$ $\displaystyle \left.\vphantom{\frac{2m+1}{2N}u\pi}\right)$ cos $\displaystyle \left(\vphantom{\frac{2n+1}{2N}v\pi}\right.$ $\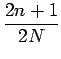displaystyle {\frac{{2n+1}}{{2N}}}$ v $\displaystyle \pi$ $\displaystyle \left.\vphantom{\frac{2n+1}{2N}v\pi}\right)$

(2.31)

2.5 La transformée en cosinus discrète

Notes