Table des matières of 2.6.2 Propriétés

Séparabilité

En permutant l'ordre d'intégration dans (2.33), nous avons

$\displaystyle \mathcal {F}$ $\displaystyle \left(\vphantom{u,v}\right.$ u, v $\displaystyle \left.\vphantom{u,v}\right)$ = $\displaystyle \int_{{-\infty}}^{{+\infty}}$ $\displaystyle \left[\vphantom{\int_{-\infty}^{+\infty}f\left(x,y\right)e^{-2\pi jxu}dx}\right.$ $\displaystyle \int_{{-\infty}}^{{+\infty}}$ f $\displaystyle \left(\vphantom{x,y}\right.$ x, y $\displaystyle \left.\vphantom{x,y}\right)$ e^-2jxudx $\displaystyle \left.\vphantom{\int_{-\infty}^{+\infty}f\left(x,y\right)e^{-2\pi jxu}dx}\right]$ e^-2jyvdy (2.41)

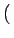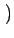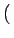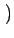La transformée de FOURIER d'une image f $\left(\vphantom{x,y}\right.$ x, y $\left.\vphantom{x,y}\right)$ peut se réaliser en deux étapes: (i) transformée de FOURIER unidimensionnelle de la fonction f $\left(\vphantom{x,y}\right.$ x, y $\left.\vphantom{x,y}\right)$ pour tout y fixé, transformant la variable x en la variable u et (ii) transformée de FOURIER unidimensionnelle de la fonction obtenue pour tout u fixé, transformant la variable y en la variable v.
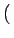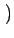Si l'image f $\left(\vphantom{x,y}\right.$ x, y $\left.\vphantom{x,y}\right)$ est spatialement séparable^2.2, c'est-à-dire

f $\displaystyle \left(\vphantom{x,y}\right.$ x, y $\displaystyle \left.\vphantom{x,y}\right)$ = f_x $\displaystyle \left(\vphantom{x}\right.$ x $\displaystyle \left.\vphantom{x}\right)$ f_y $\displaystyle \left(\vphantom{y}\right.$ y $\displaystyle \left.\vphantom{y}\right)$ (2.42)

alors

$\displaystyle \mathcal {F}$ $\displaystyle \left(\vphantom{u,v}\right.$ u, v $\displaystyle \left.\vphantom{u,v}\right)$ = $\displaystyle \mathcal {F}$ _x $\displaystyle \left(\vphantom{u}\right.$ u $\displaystyle \left.\vphantom{u}\right)$ $\displaystyle \mathcal {F}$ _y $\displaystyle \left(\vphantom{v}\right.$ v $\displaystyle \left.\vphantom{v}\right)$ (2.43)

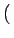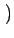Dans ce cas, la transformée de FOURIER de l'image f $\left(\vphantom{x,y}\right.$ x, y $\left.\vphantom{x,y}\right)$ est égale au produit des transformées de FOURIER unidimensionnelles des fonctions f_x $\left(\vphantom{x}\right.$ x $\left.\vphantom{x}\right)$ et f_y $\left(\vphantom{y}\right.$ y $\left.\vphantom{y}\right)$ .

Linéarité
Soient f₁ $\left(\vphantom{x,y}\right.$ x, y $\left.\vphantom{x,y}\right)$ $\rightleftharpoons$ $\mathcal {F}$ ₁ $\left(\vphantom{u,v}\right.$ u, v $\left.\vphantom{u,v}\right)$ et f₂ $\left(\vphantom{x,y}\right.$ x, y $\left.\vphantom{x,y}\right)$ $\rightleftharpoons$ $\mathcal {F}$ ₂ $\left(\vphantom{u,v}\right.$ u, v $\left.\vphantom{u,v}\right)$ . Alors, pour toutes constantes c₁ et c₂,

c₁f₁ $\displaystyle \left(\vphantom{x,y}\right.$ x, y $\displaystyle \left.\vphantom{x,y}\right)$ + c₂f₂ $\displaystyle \left(\vphantom{x,y}\right.$ x, y $\displaystyle \left.\vphantom{x,y}\right)$ $\displaystyle \rightleftharpoons$ c₁ $\displaystyle \mathcal {F}$ ₁ $\displaystyle \left(\vphantom{u,v}\right.$ u, v $\displaystyle \left.\vphantom{u,v}\right)$ + c₂ $\displaystyle \mathcal {F}$ ₂ $\displaystyle \left(\vphantom{u,v}\right.$ u, v $\displaystyle \left.\vphantom{u,v}\right)$

(2.44)

Homothétie
Si f $\left(\vphantom{x,y}\right.$ x, y $\left.\vphantom{x,y}\right)$ $\rightleftharpoons$ $\mathcal {F}$ $\left(\vphantom{u,v}\right.$ u, v $\left.\vphantom{u,v}\right)$ , alors

f $\displaystyle \left(\vphantom{ax,by}\right.$ ax, by $\displaystyle \left.\vphantom{ax,by}\right)$ $\displaystyle \rightleftharpoons$ $\displaystyle {\frac{{1}}{{\left\vert ab\right\vert}}}$ $\displaystyle \mathcal {F}$ $\displaystyle \left(\vphantom{\frac{u}{a},\frac{v}{b}}\right.$ $\displaystyle {\frac{{u}}{{a}}}$ , $\displaystyle {\frac{{v}}{{b}}}$ $\displaystyle \left.\vphantom{\frac{u}{a},\frac{v}{b}}\right)$

(2.45)

Il est à noter que l'image f $\left(\vphantom{ax,by}\right.$ ax, by $\left.\vphantom{ax,by}\right)$ correspond à l'image f $\left(\vphantom{x,y}\right.$ x, y $\left.\vphantom{x,y}\right)$ compressée dans l'espace par un facteur a dans la direction x et par un facteur b dans la direction y. Une compression dans le domaine spatial équivaut donc à une extension dans le domaine fréquentiel et vice-versa.

Dualité
Si f $\left(\vphantom{x,y}\right.$ x, y $\left.\vphantom{x,y}\right)$ $\rightleftharpoons$ $\mathcal {F}$ $\left(\vphantom{u,v}\right.$ u, v $\left.\vphantom{u,v}\right)$ , alors

$\displaystyle \mathcal {F}$ $\displaystyle \left(\vphantom{x,y}\right.$ x, y $\displaystyle \left.\vphantom{x,y}\right)$ $\displaystyle \rightleftharpoons$ f $\displaystyle \left(\vphantom{-u,-v}\right.$ - u, - v $\displaystyle \left.\vphantom{-u,-v}\right)$

(2.46)

Translation spatiale
Si f $\left(\vphantom{x,y}\right.$ x, y $\left.\vphantom{x,y}\right)$ $\rightleftharpoons$ $\mathcal {F}$ $\left(\vphantom{u,v}\right.$ u, v $\left.\vphantom{u,v}\right)$ , alors

f $\displaystyle \left(\vphantom{x-x_{0},y-y_{0}}\right.$ x - x₀, y - y₀ $\displaystyle \left.\vphantom{x-x_{0},y-y_{0}}\right)$ $\displaystyle \rightleftharpoons$ $\displaystyle \mathcal {F}$ $\displaystyle \left(\vphantom{u,v}\right.$ u, v $\displaystyle \left.\vphantom{u,v}\right)$ e^{-2jx₀u + y₀v}

(2.47)

Translation fréquentielle
Si f $\left(\vphantom{x,y}\right.$ x, y $\left.\vphantom{x,y}\right)$ $\rightleftharpoons$ $\mathcal {F}$ $\left(\vphantom{u,v}\right.$ u, v $\left.\vphantom{u,v}\right)$ , alors

f $\displaystyle \left(\vphantom{x,y}\right.$ x, y $\displaystyle \left.\vphantom{x,y}\right)$ e^{j2u₀x + v₀y} $\displaystyle \rightleftharpoons$ $\displaystyle \mathcal {F}$ $\displaystyle \left(\vphantom{u-u_{0},v-v_{0}}\right.$ u - u₀, v - v₀ $\displaystyle \left.\vphantom{u-u_{0},v-v_{0}}\right)$

(2.48)

Aires
Si f $\left(\vphantom{x,y}\right.$ x, y $\left.\vphantom{x,y}\right)$ $\rightleftharpoons$ $\mathcal {F}$ $\left(\vphantom{u,v}\right.$ u, v $\left.\vphantom{u,v}\right)$ , alors

$\displaystyle \mathcal {F}$ $\displaystyle \left(\vphantom{0,0}\right.$ 0, 0 $\displaystyle \left.\vphantom{0,0}\right)$ = $\displaystyle \int_{{-\infty}}^{{+\infty}}$ $\displaystyle \int_{{-\infty}}^{{+\infty}}$ f $\displaystyle \left(\vphantom{x,y}\right.$ x, y $\displaystyle \left.\vphantom{x,y}\right)$ dxdy

(2.49)

Le coefficient $\mathcal {F}$ $\left(\vphantom{0,0}\right.$ 0, 0 $\left.\vphantom{0,0}\right)$ , appelé parfois composante DC , est la somme des pixels de l'image. Sa dynamique est donc très importante par rapport aux autres coefficients. Ceci pose des problèmes pratiques qui amène à traiter séparément ce coefficient.

f $\displaystyle \left(\vphantom{0,0}\right.$ 0, 0 $\displaystyle \left.\vphantom{0,0}\right)$ = $\displaystyle \int_{{-\infty}}^{{+\infty}}$ $\displaystyle \int_{{-\infty}}^{{+\infty}}$ $\displaystyle \mathcal {F}$ $\displaystyle \left(\vphantom{u,v}\right.$ u, v $\displaystyle \left.\vphantom{u,v}\right)$ dudv

(2.50)

Convolution
Le produit de convolution de deux fonctions f $\left(\vphantom{x,y}\right.$ x, y $\left.\vphantom{x,y}\right)$ et g $\left(\vphantom{x,y}\right.$ x, y $\left.\vphantom{x,y}\right)$ est défini par

$\displaystyle \left(\vphantom{f\otimes g}\right.$ f $\displaystyle \otimes$ g $\displaystyle \left.\vphantom{f\otimes g}\right)$ $\displaystyle \left(\vphantom{x,y}\right.$ x, y $\displaystyle \left.\vphantom{x,y}\right)$ = $\displaystyle \int_{{-\infty}}^{{+\infty}}$ $\displaystyle \int_{{-\infty}}^{{+\infty}}$ f $\displaystyle \left(\vphantom{\alpha,\beta}\right.$ $\displaystyle \alpha$ , $\displaystyle \beta$ $\displaystyle \left.\vphantom{\alpha,\beta}\right)$ g $\displaystyle \left(\vphantom{x-\alpha,y-\beta}\right.$ x - $\displaystyle \alpha$ , y - $\displaystyle \beta$ $\displaystyle \left.\vphantom{x-\alpha,y-\beta}\right)$ d $\displaystyle \alpha$ d $\displaystyle \beta$

(2.51)

Si f $\left(\vphantom{x,y}\right.$ x, y $\left.\vphantom{x,y}\right)$ $\rightleftharpoons$ $\mathcal {F}$ $\left(\vphantom{u,v}\right.$ u, v $\left.\vphantom{u,v}\right)$ et g $\left(\vphantom{x,y}\right.$ x, y $\left.\vphantom{x,y}\right)$ $\rightleftharpoons$ $\mathcal {G}$ $\left(\vphantom{u,v}\right.$ u, v $\left.\vphantom{u,v}\right)$ , alors

$\displaystyle \left(\vphantom{f\otimes g}\right.$ f $\displaystyle \otimes$ g $\displaystyle \left.\vphantom{f\otimes g}\right)$ $\displaystyle \left(\vphantom{x,y}\right.$ x, y $\displaystyle \left.\vphantom{x,y}\right)$ $\displaystyle \rightleftharpoons$ $\displaystyle \mathcal {F}$ $\displaystyle \left(\vphantom{u,v}\right.$ u, v $\displaystyle \left.\vphantom{u,v}\right)$ $\displaystyle \mathcal {G}$ $\displaystyle \left(\vphantom{u,v}\right.$ u, v $\displaystyle \left.\vphantom{u,v}\right)$

(2.52)

La convolution de deux images dans le domaine spatial est transformée dans le domaine fréquentiel en la multiplication de leur transformée de FOURIER respective.

Multiplication
Si f $\left(\vphantom{x,y}\right.$ x, y $\left.\vphantom{x,y}\right)$ $\rightleftharpoons$ $\mathcal {F}$ $\left(\vphantom{u,v}\right.$ u, v $\left.\vphantom{u,v}\right)$ et g $\left(\vphantom{x,y}\right.$ x, y $\left.\vphantom{x,y}\right)$ $\rightleftharpoons$ $\mathcal {G}$ $\left(\vphantom{u,v}\right.$ u, v $\left.\vphantom{u,v}\right)$ , alors

f $\displaystyle \left(\vphantom{x,y}\right.$ x, y $\displaystyle \left.\vphantom{x,y}\right)$ g $\displaystyle \left(\vphantom{x,y}\right.$ x, y $\displaystyle \left.\vphantom{x,y}\right)$ $\displaystyle \rightleftharpoons$ $\displaystyle \left(\vphantom{\mathcal{F}\otimes \mathcal{G}}\right.$ $\displaystyle \mathcal {F}$ $\displaystyle \otimes$ $\displaystyle \mathcal {G}$ $\displaystyle \left.\vphantom{\mathcal{F}\otimes \mathcal{G}}\right)$ $\displaystyle \left(\vphantom{u,v}\right.$ u, v $\displaystyle \left.\vphantom{u,v}\right)$

(2.53)

La multiplication de deux images dans le domaine spatial est transformée dans le domaine fréquentiel en la convolution de leur transformée de FOURIER respective.

Notes

... séparable ^2.2

Ce n'est généralement pas le cas pour des images naturelles. Ce cas de figure peut néanmoins se produire pour certaines images de synthèse.