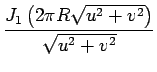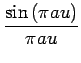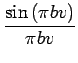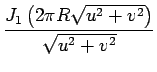Sous-sections
Considérons l'image
f x, y
x, y définie par
définie par
f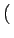 x, y x, y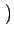 = Arect[a, b] = Arect[a, b]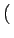 x, y x, y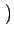 |
(2.54) |
où
Cette fonction est appelée fonction Rectangle.
L'image
f x, y
x, y vaut donc A à l'intérieur du rectangle
de longueur a et de largeur b dont les côtés sont parallèles
aux axes x et y, et zéro partout ailleurs. La transformée de
FOURIER de l'image
f
vaut donc A à l'intérieur du rectangle
de longueur a et de largeur b dont les côtés sont parallèles
aux axes x et y, et zéro partout ailleurs. La transformée de
FOURIER de l'image
f x, y
x, y est donnée par
est donnée par
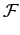 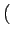 u, v u, v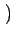 |
= |
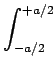 dx dx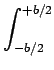 dyAe-2 dyAe-2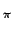 j j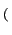 xu + yv xu + yv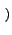 |
(2.56) |
| |
= |
Aab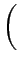 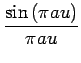 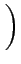 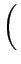 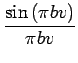 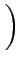 |
(2.57) |
Il s'agit du produit de deux sinus cardinaux. Ce résultat aurait pu
être obtenu en remarquant que l'image
f x, y
x, y est séparable
spatialement et en utilisant la propriété 2.43
de séparabilité. Nous avons donc la paire de transformées de FOURIER
est séparable
spatialement et en utilisant la propriété 2.43
de séparabilité. Nous avons donc la paire de transformées de FOURIER
Une représentation de l'image
f x, y
x, y est donné à la
figure 2.4 tandis que le module de sa transformée
de FOURIER est représenté à la figure 2.5.
est donné à la
figure 2.4 tandis que le module de sa transformée
de FOURIER est représenté à la figure 2.5.
Figure 2.4:
Illustration de la fonction Rectangle.
|
|
Figure 2.5:
Module de la transformée de FOURIER de la fonction Rectangle.
|
|
Considérons l'image
f x, y
x, y définie par
définie par
f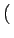 x, y x, y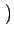 = ADisqueR = ADisqueR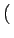 x, y x, y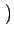 |
(2.59) |
où
est appelée fonction disque.
L'image
f x, y
x, y vaut donc A sur le disque de rayon
R et zéro partout ailleurs. La transformée de FOURIER
de l'image
f
vaut donc A sur le disque de rayon
R et zéro partout ailleurs. La transformée de FOURIER
de l'image
f x, y
x, y est donnée par
est donnée par
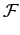 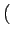 u, v u, v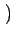 |
= |
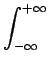 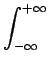 f f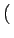 x, y x, y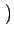 e-2 e-2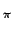 j j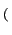 xu + yv xu + yv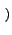 dxdy dxdy |
(2.61) |
| |
= |
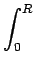 rdr rdr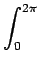 Ae-2 Ae-2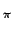 jr jr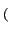 u cos u cos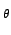 + v sin + v sin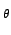 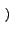 d d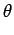 |
(2.62) |
où nous avons effectué un changement de variables des coordonnées
cartésiennes vers les coordonnées polaires. En se basant sur les propriétés
des fonctions de BESSEL, nous obtenons le résultat suivant
où
J1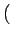 r
r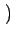 est la fonction de BESSEL d'ordre
1. Il est à noter que la transformée de FOURIER de l'image
f
est la fonction de BESSEL d'ordre
1. Il est à noter que la transformée de FOURIER de l'image
f x, y
x, y est purement réelle et à symétrie radiale, c'est-à-dire
qu'elle ne dépend que de la distance
est purement réelle et à symétrie radiale, c'est-à-dire
qu'elle ne dépend que de la distance
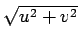 à l'origine.
Nous avons donc la paire de transformées de FOURIER
à l'origine.
Nous avons donc la paire de transformées de FOURIER
L'image
f x, y
x, y est représentée à la figure 2.6
tandis que le module de sa transformée de FOURIER est représenté
à la figure 2.7.
est représentée à la figure 2.6
tandis que le module de sa transformée de FOURIER est représenté
à la figure 2.7.
Figure 2.6:
Illustration de la fonction Disque.
|
|
Figure 2.7:
Module de la transformée de FOURIER de la fonction Disque.
|
|
Pour rappel, nous avons la paire de transformées de FOURIER
suivante
En utilisant la propriété de dualité (relation 2.46)
de la transformée de FOURIER, nous obtenons
La nouvelle image ainsi obtenue est dite à bande limitée car son spectre
en fréquence est limité à une région finie du plan u - v. En l'occurrence,
cette région est, dans ce cas-ci, un rectangle de longueur a et
de largeur b centré à l'origine. D'après la définition de la fonction
rectangle, le spectre est nul en dehors de ce rectangle.
Pour rappel, nous avons la paire de transformées de FOURIER
suivante
En utilisant la propriété de dualité (relation 2.46)
de la transformée de FOURIER, nous obtenons
La nouvelle image ainsi obtenue est à bande limitée. Dans ce cas,
le spectre est limité au disque de rayon f0 centré à l'origine.
f0 est appelée fréquence radiale de coupure.
Marc Van Droogenbroeck. Tous droits réservés.
2003-09-30
![]() x, y
x, y![]() définie par
définie par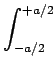 dx
dx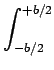 dyAe-2
dyAe-2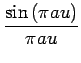
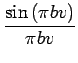
![]() x, y
x, y![]() est donné à la
figure 2.4 tandis que le module de sa transformée
de FOURIER est représenté à la figure 2.5.
est donné à la
figure 2.4 tandis que le module de sa transformée
de FOURIER est représenté à la figure 2.5.
![]() x, y
x, y![]() définie par
définie par