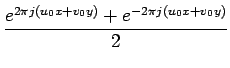Sous-sections
Il est possible de donner une autre définition équivalente de l'impulsion
de DIRAC qui englobe les équations 2.69
et 2.70
  f f x, y x, y  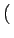 x - x - 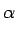 , y - , y - 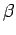 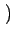 dxdy = f dxdy = f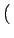 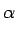 , ,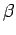 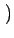 |
(2.71) |
où
f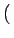 x, y
x, y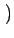 est une fonction continue de x et y.
est une fonction continue de x et y.
La fonction
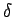
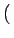 x, y
x, y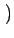 est spatialement séparable en
deux fonctions de DIRAC à une dimension
est spatialement séparable en
deux fonctions de DIRAC à une dimension
Étant donné que la fonction
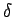
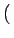 x, y
x, y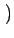 est une fonction
symétrique par rapport à l'origine, l'équation (2.71)
peut encore s'écrire, en changeant les variables d'intégration, sous
la forme
est une fonction
symétrique par rapport à l'origine, l'équation (2.71)
peut encore s'écrire, en changeant les variables d'intégration, sous
la forme
  f f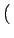 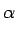 , ,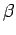 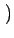 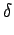 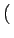 x - x - 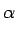 , y - , y - 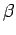 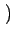 d d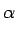 d d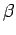 = f = f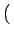 x, y x, y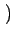 |
(2.73) |
Le membre de gauche de l'équation 2.73 représente
le produit de convolution de
f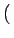 x, y
x, y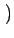 par
par
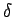
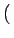 x, y
x, y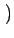 .
On peut donc écrire
.
On peut donc écrire
f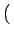 x, y x, y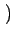 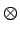 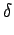 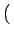 x, y x, y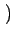 = f = f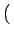 x, y x, y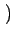 |
(2.74) |
Dès lors, la convolution d'une fonction
f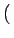 x, y
x, y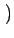 avec
l'impulsion de DIRAC laisse cette fonction inchangée.
avec
l'impulsion de DIRAC laisse cette fonction inchangée.
Par définition, la transformée de FOURIER de
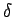
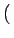 x, y
x, y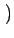 est donnée par
est donnée par
  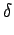 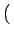 x, y x, y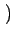 e-2 e-2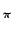 j j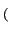 xu + yv xu + yv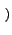 dxdy dxdy |
(2.75) |
Étant donné que la fonction
e-2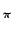 j
j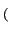 xu + yv
xu + yv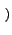 évaluée
en l'origine
évaluée
en l'origine
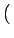 0, 0
0, 0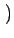 vaut 1, il vient finalement
vaut 1, il vient finalement
Donc, le spectre en fréquence de l'impulsion de DIRAC s'étend
uniformément sur tout l'intervalle fréquentiel
 -
- 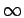 , +
, + 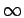
![$ \left.\vphantom{-\infty,+\infty}\right]$](img247.gif) ×
× -
- 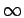 , +
, + 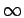
![$ \left.\vphantom{-\infty,+\infty}\right]$](img247.gif) .
.
- Image continue
En utilisant la propriété de dualité (relation 2.46)
de la transformée de FOURIER et étant donné que
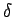
 x, y
x, y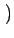 est symétrique par rapport à l'origine, on peut écrire
est symétrique par rapport à l'origine, on peut écrire
Le spectre d'une image continue est donc discret et comporte une
seule raie située à l'origine
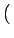 0, 0
0, 0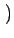 du plan
u - v.
du plan
u - v.
- Image complexe exponentielle
En appliquant la propriété de translation fréquentielle (relation 2.48)
de la transformée de FOURIER à 2.77,
il vient
e-2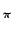 j j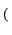 u0x + v0x u0x + v0x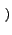 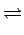 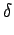 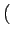 u - u0, v - v0 u - u0, v - v0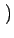 |
(2.78) |
Le spectre d'une image complexe exponentielle de fréquence
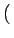 u0, v0
u0, v0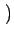 se limite donc à une raie située en
se limite donc à une raie située en
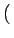 u0, v0
u0, v0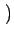 dans le plan u - v.
dans le plan u - v.
- Image sinusoïdale
Soit l'image
cos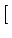 2
2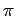
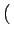 u0x + v0y
u0x + v0y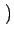
![$ \left.\vphantom{2\pi\left(u_{0}x+v_{0}y\right)}\right]$](img344.gif) . Rappelons
tout d'abord la formule bien connue
. Rappelons
tout d'abord la formule bien connue
En utilisant la relation 2.78
et la propriété de linéarité de la transformée de FOURIER,
il vient
Le spectre d'une image cosinusoïdale comporte donc 2 raies situées
en
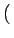 u0, v0
u0, v0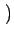 et
et
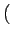 - u0, - v0
- u0, - v0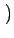 dans
le plan u - v. Il est également aisé de montrer que
dans
le plan u - v. Il est également aisé de montrer que
Marc Van Droogenbroeck. Tous droits réservés.
2003-09-30
![]()
![]() x, y
x, y![]() est spatialement séparable en
deux fonctions de DIRAC à une dimension
est spatialement séparable en
deux fonctions de DIRAC à une dimension![]()
![]() x, y
x, y![]() est une fonction
symétrique par rapport à l'origine, l'équation (2.71)
peut encore s'écrire, en changeant les variables d'intégration, sous
la forme
est une fonction
symétrique par rapport à l'origine, l'équation (2.71)
peut encore s'écrire, en changeant les variables d'intégration, sous
la forme ![]()
![]() x, y
x, y![]() est donnée par
est donnée par