Considérons une fonction
f![]() x, y
x, y![]() connue pour tout x
et y. Supposons que cette fonction soit échantillonnée uniformément
de manière rectangulaire. Nous disposons ainsi d'une infinité d'échantillons
de
f
connue pour tout x
et y. Supposons que cette fonction soit échantillonnée uniformément
de manière rectangulaire. Nous disposons ainsi d'une infinité d'échantillons
de
f![]() x, y
x, y![]() espacés de
espacés de ![]() x dans la direction de
l'axe x et de
x dans la direction de
l'axe x et de ![]() y dans la direction de l'axe y.
y dans la direction de l'axe y. ![]() x
et
x
et ![]() y sont appelées pas d'échantillonnage
selon x et y respectivement. Les échantillons sont alors notés
f
y sont appelées pas d'échantillonnage
selon x et y respectivement. Les échantillons sont alors notés
f![]() i
i![]() x, j
x, j![]() y
y![]() où i et j sont des nombres
entiers.
où i et j sont des nombres
entiers.
![]() et
et
![]() sont appelées
fréquences d'échantillonnage
selon x et y respectivement.
sont appelées
fréquences d'échantillonnage
selon x et y respectivement.
Introduisons à présent la fonction d'échantillonnage idéale définie par
Établissons à présent le lien entre les échantillons
f![]() i
i![]() x, j
x, j![]() y
y![]() et la fonction d'échantillonnage idéale.
et la fonction d'échantillonnage idéale.
Déterminons à présent la relation existant entre les transformées
de FOURIER respectives de
fs![]() x, y
x, y![]() et
f
et
f![]() x, y
x, y![]() .
Pour cela, nous partons de la relation 2.83 et nous
utilisons les propriétés de la fonction de DIRAC
.
Pour cela, nous partons de la relation 2.83 et nous
utilisons les propriétés de la fonction de DIRAC
| fs |
= | (2.84) | |
| = | f |
(2.85) | |
| = | f |
(2.86) |
La fonction échantillonnée idéale est donc égale au produit de la
fonction
f![]() x, y
x, y![]() et de la fonction d'échantillonnage
idéale dans le domaine spatial. En utilisant la propriété de multiplication
(relation 2.53) de la transformée
de FOURIER, il vient
et de la fonction d'échantillonnage
idéale dans le domaine spatial. En utilisant la propriété de multiplication
(relation 2.53) de la transformée
de FOURIER, il vient
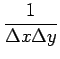 |
(2.88) |
| = | (2.89) | ||
| = | 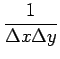 |
||
| = | 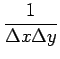 |
||
| = | 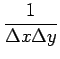 |
(2.90) |
Ce résultat est particulièrement intéressant: mis à part le facteur
1/![]() x
x![]() y, la transformée de FOURIER de la fonction
échantillonnée
fs
y, la transformée de FOURIER de la fonction
échantillonnée
fs![]() x, y
x, y![]() est obtenue par la répétition
de celle de
f
est obtenue par la répétition
de celle de
f![]() x, y
x, y![]() à tous les multiples de la fréquence
d'échantillonnage
à tous les multiples de la fréquence
d'échantillonnage
![]() 1/
1/![]() x, 1/
x, 1/![]() y
y![]() . Elle est
donc périodique de période fondamentale
. Elle est
donc périodique de période fondamentale
![]() 1/
1/![]() x, 1/
x, 1/![]() y
y![]() .
.
Comme pour le cas des signaux unidimensionnels, il existe un théorème de SHANNON permettant d'éviter le recouvrement des copies du spectre occasionné par un sous-échantillonnage; ce phénomène porte le nom de repli de spectre ou d'aliasing. Afin d'illustrer ce théorème, considérons la fonction suivante
g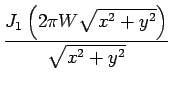 |
(2.92) |
Supposons que
g![]() x, y
x, y![]() soit échantillonnée à la fréquence
soit échantillonnée à la fréquence
![]() 1/
1/![]() x, 1/
x, 1/![]() y
y![]() . La transformée de FOURIER
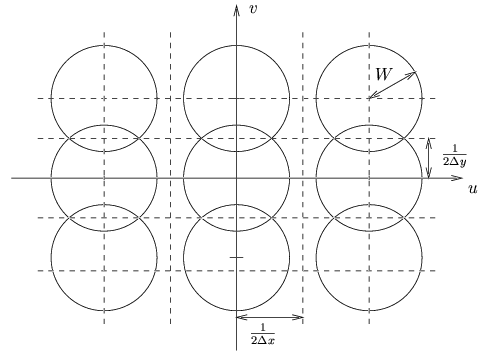
de la fonction échantillonnée correspondante est représentée à la
figure 2.9. Sur cette figure, on peut remarquer qu'il
y a recouvrement du spectre dans la direction v mais pas dans la
direction u.
. La transformée de FOURIER
de la fonction échantillonnée correspondante est représentée à la
figure 2.9. Sur cette figure, on peut remarquer qu'il
y a recouvrement du spectre dans la direction v mais pas dans la
direction u.
|
Nous pouvons à présent énoncer le théorème de SHANNON. Soit
umax et vmax les fréquences maximales d'une fonction
f![]() x, y
x, y![]() dans les directions x et y respectivement. On suppose donc que
l'image
f
dans les directions x et y respectivement. On suppose donc que
l'image
f![]() x, y
x, y![]() est à bande limitée.
est à bande limitée.