4.4 Les transformations de voisinage

Considérons un ensemble discret X. Le voisinage d'un point ne sera rien d'autre que le carré composé de 9 pixels, centré sur ce point. Si l'on attribue la valeur 1 ou 0 à chacun des points constituant le carré élémentaire, on forme une configuration de voisinage. Chacune de ces configurations constitue un élément structurant $\nu^{{i}}_{}$, associé au réseau considéré. Dans le cas du réseau carré, il existe 2⁹ configurations possibles. Dans la plupart des algorithmes utilisant des configurations de voisinage, elles sont groupées en famille $\nu$ = {$\nu^{{1}}_{}$, $\nu^{{2}}_{}$, ..., $\nu^{{n}}_{}$}.

Appelant $\nu_{{x}}^{}$ la configuration de voisinage centrée en x, on définit une transformation de voisinage par la transformation qui attribue la valeur 1 (c'est la construction de la fonction indicatrice ^4.3) à chaque point ayant une configuration semblable à un élément de la famille de configurations $\nu$:

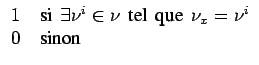$$\bigtriangledown \nu \left\{\vphantom{ \begin{array}{ll} 1 & \,\textrm{si}\,\textrm{ }... ...trm{ que}\,\textrm{ }\nu_{x}=\nu^{i}\\ 0 & \,\textrm{sinon}\end{array}}\right. \begin{array}{ll} 1 & \,\textrm{si}\,\textrm{ }\exists\nu^{i}\in\... ...l}\,\textrm{ que}\,\textrm{ }\nu_{x}=\nu^{i}\\ 0 & \,\textrm{sinon}\end{array}$$ (4.25)

Cette transformation satisfait les principes des transformations morphologiques énoncés précédemment.

L'érosion par un élément structurant n'est qu'un cas particulier de transformation de voisinage; elle revient à une transformation de voisinage où $\nu$ = {$\nu^{{i}}_{}$| B $\subseteq$ $\nu^{{i}}_{}$}.

Il existe aussi une transformation de voisinage appelée transformée par tout ou rien (Hit or Miss transform en anglais) telle que

$$\Uparrow \subseteq \subseteq$$ (4.26)

Si C = $\emptyset$ la transformation dégénère en une opération d'érosion de X par B.

Les transformations de voisinage sont donc plus générales que les transformations morphologiques décrites précédemment, mais compte tenu de leur généralité, on ne peut leur associer aucune propriété fondamentale; elles dépendent de la configuration choisie.

Notes

...indicatrice ^4.3

La fonction indicatrice prend la valeur 1 si le point appartient à l'ensemble et 0 dans le cas contraire. Ce n'est, somme toute, qu'un autre moyen de définir un ensemble en extension.