Sous-sections

4.3.4 Modulation de phase numérique (Phase Shift Keying)

4.3.4.1 Description

Bien que la modulation PSK soit une modulation de phase, nous allons montrer que ce type de modulation fait partie intégrante des modulations linéaires classiques. Typiquement, un signal modulé PSK a la forme

s(t) = A $\displaystyle \sum_{{k=-\infty}}^{{+\infty}}$rect[0, T]$\displaystyle \left(\vphantom{t-kT}\right.$t - kT$\displaystyle \left.\vphantom{t-kT}\right)$ cos$\displaystyle \left(\vphantom{2\pi f_{c}t+\varphi_{c}+\psi_{k}}\right.$2$\displaystyle \pi$fct + $\displaystyle \varphi_{{c}}^{}$ + $\displaystyle \psi_{{k}}^{}$$\displaystyle \left.\vphantom{2\pi f_{c}t+\varphi_{c}+\psi_{k}}\right)$ (4.37)

où $ \psi_{{k}}^{}$ est une variable aléatoire constante sur l'intervalle de temps $ \left[\vphantom{kT, (k+1)T}\right.$kT, (k + 1)T$ \left.\vphantom{kT, (k+1)T}\right[$ , pouvant prendre N valeurs possibles D

$\displaystyle \psi_{{k}}^{}$ $\displaystyle \in$ $\displaystyle \left\{\vphantom{ \psi\left\vert\psi=\varphi_{0}+i\frac{2\pi}{N}, i=0, ..., N-1\right.}\right.$$\displaystyle \psi$$\displaystyle \left\vert\vphantom{\psi=\varphi_{0}+i\frac{2\pi}{N}, i=0, ..., N-1}\right.$$\displaystyle \psi$ = $\displaystyle \varphi_{{0}}^{}$ + i$\displaystyle {\frac{{2\pi}}{{N}}}$, i = 0, ..., N - 1$\displaystyle \left.\vphantom{ \psi\left\vert\psi=\varphi_{0}+i\frac{2\pi}{N}, i=0, ..., N-1\right.}\right\}$ (4.38)

Le signal modulé a donc une enveloppe constante et subit un saut de phase toutes les T secondes.

Cherchons à présent à faire le lien avec les modulations linéaires classiques. Pour cela, nous réécrivons s(t) sous la forme

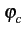s(t) = A$\displaystyle \sum_{{k=-\infty}}^{{+\infty}}$rect[0, T]$\displaystyle \left(\vphantom{t-kT}\right.$t - kT$\displaystyle \left.\vphantom{t-kT}\right)$ $\displaystyle \left[\vphantom{\cos\left(2\pi f_{c}t+\varphi_{c}\right)\cos\psi_{k}-\sin\left(2\pi f_{c}t+\varphi_{c}\right)\sin\psi_{k}}\right.$cos$\displaystyle \left(\vphantom{2\pi f_{c}t+\varphi_{c}}\right.$2$\displaystyle \pi$fct + $\displaystyle \varphi_{{c}}^{}$$\displaystyle \left.\vphantom{2\pi f_{c}t+\varphi_{c}}\right)$cos$\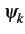displaystyle \psi_{{k}}^{}$ - sin$\displaystyle \left(\vphantom{2\pi f_{c}t+\varphi_{c}}\right.$2$\displaystyle \pi$fct + $\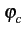displaystyle \varphi_{{c}}^{}$$\displaystyle \left.\vphantom{2\pi f_{c}t+\varphi_{c}}\right)$sin$\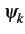displaystyle \psi_{{k}}^{}$$\displaystyle \left.\vphantom{\cos\left(2\pi f_{c}t+\varphi_{c}\right)\cos\psi_{k}-\sin\left(2\pi f_{c}t+\varphi_{c}\right)\sin\psi_{k}}\right]$  
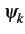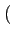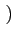  = $\displaystyle \left[\vphantom{\sum_{k=-\infty}^{+\infty}A \cos\psi_{k} \textrm{rect}_{[0,T]}\left(t-kT\right)}\right.$$\displaystyle \sum_{{k=-\infty}}^{{+\infty}}$A cos$\displaystyle \psi_{{k}}^{}$ rect[0, T]$\displaystyle \left(\vphantom{t-kT}\right.$t - kT$\displaystyle \left.\vphantom{t-kT}\right)$$\displaystyle \left.\vphantom{\sum_{k=-\infty}^{+\infty}A \cos\psi_{k} \textrm{rect}_{[0,T]}\left(t-kT\right)}\right]$ cos$\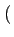displaystyle \left(\vphantom{2\pi f_{c}t+\varphi_{c}}\right.$2$\displaystyle \pi$fct + $\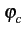displaystyle \varphi_{{c}}^{}$$\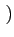displaystyle \left.\vphantom{2\pi f_{c}t+\varphi_{c}}\right)$ (4.39)
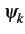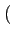    - $\displaystyle \left[\vphantom{\sum_{k=-\infty}^{+\infty}A \sin\psi_{k} \textrm{rect}_{[0,T]}\left(t-kT\right)}\right.$$\displaystyle \sum_{{k=-\infty}}^{{+\infty}}$A sin$\displ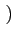aystyle \psi_{{k}}^{}$ rect[0, T]$\displaystyle \left(\vphantom{t-kT}\right.$t - kT$\displaystyle \left.\vphantom{t-kT}\right)$$\displaystyle \left.\vphantom{\sum_{k=-\infty}^{+\infty}A \sin\psi_{k} \textrm{rect}_{[0,T]}\left(t-kT\right)}\right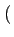]$ sin$\displaystyle \left(\vphantom{2\pi f_{c}t+\varphi_{c}}\right.$2$\displaystyle \pi$fct + $\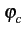displaystyle \varphi_{{c}}^{}$$\displaystyle \left.\vphantom{2\pi f_{c}t+\varphi_{c}}\right)$ (4.40)

L'enveloppe complexe du signal s'en déduit donc
es(t) = sI(t) + j sQ(t) (4.41)
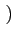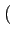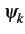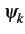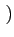  = A$\displaystyle \sum_{{k=-\infty}}^{{+\infty}}$rect[0, T]$\displaystyle \left(\vphantom{t-kT}\right.$t - kT$\displaystyle \left.\vphantom{t-kT}\right)$ $\displaystyle \left(\vphantom{\cos\psi_{k}+j\sin\psi_{k}}\right.$cos$\displaystyle \psi_{{k}}^{}$ + j sin$\displaystyle \psi_{{k}}^{}$$\displaystyle \left.\vphantom{\cos\psi_{k}+j\sin\psi_{k}}\right)$ (4.42)

Nous retrouvons donc bien l'expression générale de l'enveloppe complexe d'un signal numérique linéaire classique pour lequel
Dk = A ej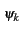$\scriptstyle \psi_{{k}}$ (4.43)
g(t) = rect[0, T]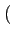$\displaystyle \left(\vphantom{t}\right.$t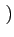$\displaystyle \left.\vphantom{t}\right)$ (4.44)

Il est alors aisé de déterminer l'enveloppe et la phase du signal modulé :
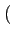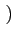a(t) = A$\displaystyle \sum_{{k=-\infty}}^{{+\infty}}$rect[0, T]$\displaystyle \left(\vphantom{t-kT}\right.$t - kT$\displaystyle \left.\vphantom{t-kT}\right)$ (4.45)
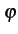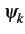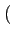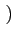$\displaystyle \varphi$(t) = $\displaystyle \sum_{{k=-\infty}}^{{+\infty}}$$\displaystyle \psi_{{k}}^{}$ rect[0, T]$\displaystyle \left(\vphantom{t-kT}\right.$t - kT$\displaystyle \left.\vphantom{t-kT}\right)$ (4.46)

Nous retrouvons bien évidemment que l'enveloppe du signal modulé est constante et que la phase varie par paliers de manière discontinue.

4.3.4.2 Cas particulier: modulation PSK-2 ou BPSK

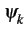
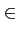
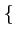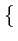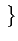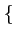
La modulation BPSK est une modulation à 2 états correspondant à $ \psi_{{k}}^{}$ $ \in$ $ \left\{\vphantom{ 0,\pi}\right.$0,$ \pi$$ \left.\vphantom{ 0,\pi}\right\}$ . 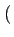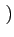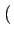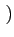La variable aléatoire Dk peut donc prendre les valeurs $ \left\{\vphantom{ A e^{j0}, A e^{j\pi}}\right.$A ej0, A ej$\scriptstyle \pi$$ \left.\vphantom{ A e^{j0}, A e^{j\pi}}\right\}$ , ce qui correspond à $ \left\{\vphantom{ \left(A,0\right), \left(-A,0\right)}\right.$$ \left(\vphantom{A,0}\right.$A, 0$ \left.\vphantom{A,0}\right)$, $ \left(\vphantom{-A,0}\right.$ - A, 0$ \left.\vphantom{-A,0}\right)$$ \left.\vphantom{ \left(A,0\right), \left(-A,0\right)}\right\}$ . La modulation BPSK correspond ainsi exactement à la modulation ASK-2. Son plan de constellations est donc également celui de la figure 4.1.

4.3.4.2.1 Densité spectrale de puissance.

Les modulations ASK-2 et BPSK étant identiques, elles ont même densité spectrale de puissance (T = Tb ). Elle est exprimée par

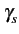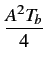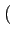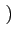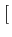$\displaystyle \gamma_{{s}}^{}$(f )= $\displaystyle {\frac{{A^{2}T_{b}}}{{4}}}$$\displaystyle \left\{\vphantom{ sinc^{2}\left[\left(f-f_{c}\right)T_{b}\right]+sinc^{2}\left[\left(f+f_{c}\right)T_{b}\right]}\right.$sinc2$\displaystyle \left[\vphantom{\left(f-f_{c}\right)T_{b}}\right.$$\displaystyle \left(\vphantom{f-f_{c}}\right.$f - fc$\displaystyle \left.\vphantom{f-f_{c}}\right)$Tb$\displaystyle \left.\vphantom{\left(f-f_{c}\right)T_{b}}\right]$ + sinc2$\displaystyle \left[\vphantom{\left(f+f_{c}\right)T_{b}}\right.$$\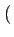displaystyle \left(\vphantom{f+f_{c}}\right.$f + fc$\displaystyle \left.\vphantom{f+f_{c}}\right)$Tb$\displaystyle \left.\vphantom{\left(f+f_{c}\right)T_{b}}\right]$$\displaystyle \left.\vphantom{ sinc^{2}\left[\left(f-f_{c}\right)T_{b}\right]+sinc^{2}\left[\left(f+f_{c}\right)T_{b}\right]}\right\}$ (4.47)

Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27