par rapport à la modulation QPSK. La figure 4.7
illustre la formation de ces séquences pour un signal de mise en forme
égal à
g(t) = rect[0, T]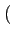 t t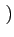 = rect[0, 2Tb] = rect[0, 2Tb]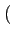 t t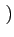 |
(4.87) |
qui correspond à modulation OQPSK classique.
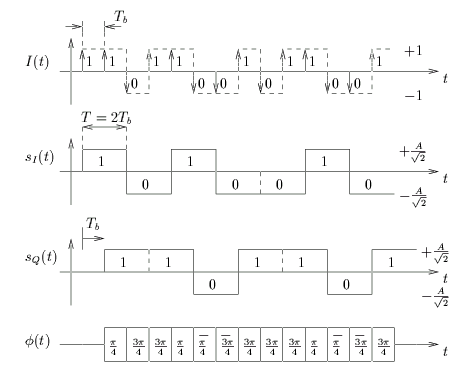
Figure 4.7:
Formation des composantes en phase et en quadrature pour la modulation
OQPSK (avec une mise en forme par un signal rectangulaire).
|
|
Il est maintenant nettement moins évident de calculer l'enveloppe
et la phase instantanée du signal modulé, cela à cause du ``chevauchement''
entre les impulsions de sI(t)
et sQ(t)
. En toute généralité,
nous pouvons écrire
a(t) = 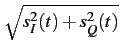 |
(4.88) |
pour l'enveloppe instantanée et
pour la phase instantanée. En observant la figure 4.7,
nous pouvons déduire que l'enveloppe du signal modulé est constante,
sauf peut-être aux transitions des signaux sI(t)
et sQ(t)
,
c'est-à-dire toutes les Tb
secondes. La phase, quant à elle,
varie toujours par paliers; pour s'en convaincre, il suffit à nouveau
de se référer au plan de constellations de la figure 4.2.
Deux différences essentielles sont cependant à remarquer. Tout d'abord,
la phase ne change plus de valeur toutes les T = 2Tb
secondes
comme dans la modulation QPSK mais bien toutes les Tb
secondes.
De plus, il n'y a plus, à chaque transition de la phase, qu'un saut
de
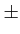
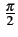 . Le fait de décaler la séquence sI(t)
a fait disparaître les transitions de
. Le fait de décaler la séquence sI(t)
a fait disparaître les transitions de 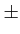
 . En effet, dans la
modulation QPSK, les transitions de
. En effet, dans la
modulation QPSK, les transitions de 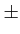
 étaient dues aux transitions
simultanées des signaux sI(t)
et sQ(t)
. Dans la modulation
OQPSK, ces deux signaux ne varient jamais en même temps. Les transitions
possibles sont représentées en pointillés sur la figure 4.8.
Celles-ci ne se faisant plus qu'horizontalement ou verticalement,
l'enveloppe du signal modulé ne peut donc plus s'annuler, ce qui est
un gros avantage de la modulation OQPSK par rapport à la modulation
QPSK.
étaient dues aux transitions
simultanées des signaux sI(t)
et sQ(t)
. Dans la modulation
OQPSK, ces deux signaux ne varient jamais en même temps. Les transitions
possibles sont représentées en pointillés sur la figure 4.8.
Celles-ci ne se faisant plus qu'horizontalement ou verticalement,
l'enveloppe du signal modulé ne peut donc plus s'annuler, ce qui est
un gros avantage de la modulation OQPSK par rapport à la modulation
QPSK.
La figure 4.9 montre un signal modulé OQPSK pour une
séquence binaire donnée.
Figure 4.8:
Diagramme de constellations pour la modulation OQPSK.
|
|
Figure:
Illustration de la modulation OQPSK: (a) séquence binaire I(t)
,
(b) sI(t)
, (c) sQ(t)
, (d)
sI(t) cos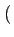 2
2 fct
fct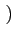 ,
(e)
sQ(t) sin
,
(e)
sQ(t) sin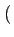 2
2 fct
fct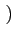 et (f) signal modulé
s(t)
.
et (f) signal modulé
s(t)
.
|
|
Les circuits de modulation et de démodulation pour l'OQPSK sont tout
à fait semblables à ceux utilisés pour le QPSK, mis à part un délai
de Tb
qu'il faut introduire dans la branche en quadrature des
circuits.
L'enveloppe complexe du signal modulé est donnée par
es(t) =  Ak g(t - kTb) ejk Ak g(t - kTb) ejk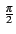 |
(4.90) |
où le signal de mise en forme g(t)
et la variable aléatoire Ak
valent respectivement
| g(t) |
= |
rect[0, 2Tb]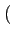 t t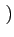 |
(4.91) |
| Ak |
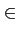 |
 + + 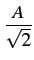 , - , - 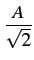 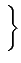 |
(4.92) |
Nous faisons à nouveau l'hypothèse que les deux valeurs possibles
pour Ak
sont équiprobables. La moyenne 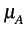 est donc nulle
et la variance est égale à
est donc nulle
et la variance est égale à
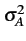 = E
= E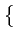 Ak2
Ak2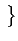 =
= 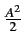 .
Il vient après calcul de la transformée de FOURIER du signal
de mise en forme
.
Il vient après calcul de la transformée de FOURIER du signal
de mise en forme
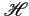 (f )=
(f )= 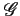
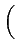 f +
f + 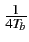
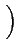 ,
,
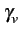 (f )= 2A2Tb sinc2 (f )= 2A2Tb sinc2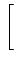 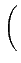 f + f + 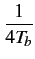 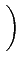 2Tb 2Tb![$\displaystyle \left.\vphantom{\left(f+\frac{1}{4T_{b}}\right)2T_{b}}\right]$](img781.gif) |
(4.93) |
Conformément à la relation (4.78), la densité
spectrale de puissance d'un signal modulé en OQPSK s'exprime donc
finalement par
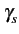 (f )= (f )= 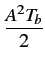 ![$\displaystyle \left\{\vphantom{ sinc^{2}\left[\left(f-f_{c}\right)2T_{b}\right]+sinc^{2}\left[\left(f+f_{c}\right)2T_{b}\right]}\right.$](img715.gif) sinc2 sinc2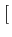 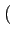 f - fc f - fc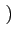 2Tb 2Tb![$\displaystyle \left.\vphantom{\left(f-f_{c}\right)2T_{b}}\right]$](img717.gif) + sinc2 + sinc2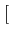 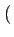 f + fc f + fc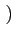 2Tb 2Tb![$\displaystyle \left.\vphantom{\left(f+f_{c}\right)2T_{b}}\right]$](img719.gif) ![$\displaystyle \left.\vphantom{ sinc^{2}\left[\left(f-f_{c}\right)2T_{b}\right]+sinc^{2}\left[\left(f+f_{c}\right)2T_{b}\right]}\right\}$](img720.gif) |
(4.94) |
et est exactement identique à celle d'un signal modulé QPSK.
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27
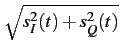
![]() (t) = arctan
(t) = arctan![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 2
2![]() fct
fct![]()
![]() 2
2![]() fct
fct![]()
![\includegraphics[width=13cm]{images/oqpsk}](img773.gif)
![]() Ak g(t - kTb) ejk
Ak g(t - kTb) ejk![]()
![]() t
t![]()
![]()
![]() +
+ ![]() , -
, - ![]()
![]()
![]()
![]() = E
= E![]() Ak2
Ak2![]() =
= ![]()
![]() (f )=
(f )= ![]()
![]() f +
f + ![]()
![]()
![]() (f )= 2A2Tb sinc2
(f )= 2A2Tb sinc2![]()
![]() f +
f + ![]()
![]() 2Tb
2Tb![]()